
Question Number 215280 by universe last updated on 02/Jan/25
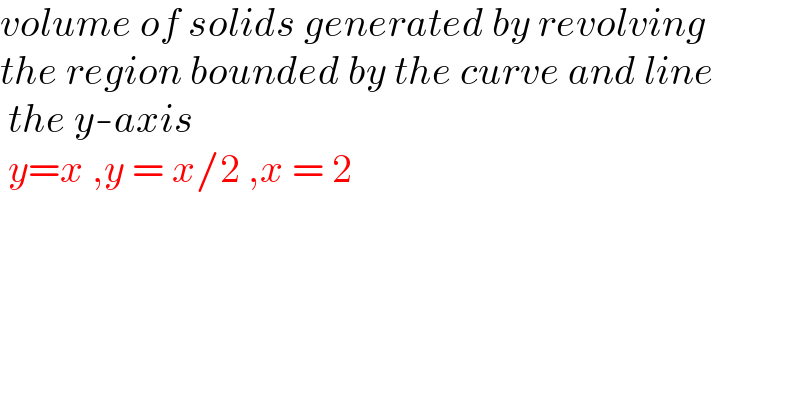
$${volume}\:{of}\:{solids}\:{generated}\:{by}\:{revolving} \\ $$$${the}\:{region}\:{bounded}\:{by}\:{the}\:{curve}\:{and}\:{line} \\ $$$$\:{the}\:{y}-{axis} \\ $$$$\:{y}={x}\:,{y}\:=\:{x}/\mathrm{2}\:,{x}\:=\:\mathrm{2} \\ $$
Commented by mr W last updated on 02/Jan/25
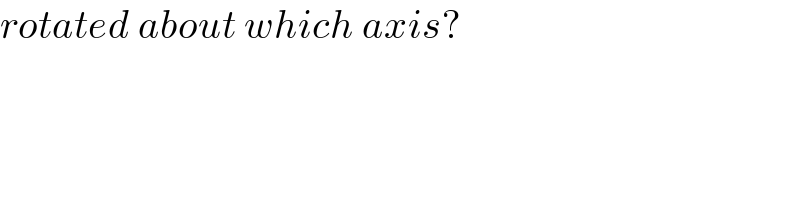
$${rotated}\:{about}\:{which}\:{axis}? \\ $$
Commented by universe last updated on 02/Jan/25

$${y}\:−{axis} \\ $$
Answered by MrGaster last updated on 02/Jan/25
![V=π∫_a ^b [f(x)]^2 −[g(x)]^2 dx V=π∫_0 ^2 [x]^2 −[(π/2)]^2 dx V=π∫_0 ^2 x^2 −(x^2 /4)dx V=π∫_0 ^2 ((4x^2 )/4)−(x^2 /4)dx V=π∫_0 ^2 ((3x^2 )/4)dx V=π[((3x^3 )/(12))]_0 ^2 V=π(((3∙2^3 )/(12))−((3∙0^3 )/(12))) V=π(((3∙8)/(12))) V=π(((24)/(12))) V=2π](Q215281.png)
$${V}=\pi\int_{{a}} ^{{b}} \left[{f}\left({x}\right)\right]^{\mathrm{2}} −\left[{g}\left({x}\right)\right]^{\mathrm{2}} {dx} \\ $$$${V}=\pi\int_{\mathrm{0}} ^{\mathrm{2}} \left[{x}\right]^{\mathrm{2}} −\left[\frac{\pi}{\mathrm{2}}\right]^{\mathrm{2}} {dx} \\ $$$${V}=\pi\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{4}}{dx} \\ $$$${V}=\pi\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}{dx} \\ $$$${V}=\pi\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}{dx} \\ $$$${V}=\pi\left[\frac{\mathrm{3}{x}^{\mathrm{3}} }{\mathrm{12}}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$${V}=\pi\left(\frac{\mathrm{3}\centerdot\mathrm{2}^{\mathrm{3}} }{\mathrm{12}}−\frac{\mathrm{3}\centerdot\mathrm{0}^{\mathrm{3}} }{\mathrm{12}}\right) \\ $$$${V}=\pi\left(\frac{\mathrm{3}\centerdot\mathrm{8}}{\mathrm{12}}\right) \\ $$$${V}=\pi\left(\frac{\mathrm{24}}{\mathrm{12}}\right) \\ $$$${V}=\mathrm{2}\pi \\ $$
Answered by mr W last updated on 02/Jan/25
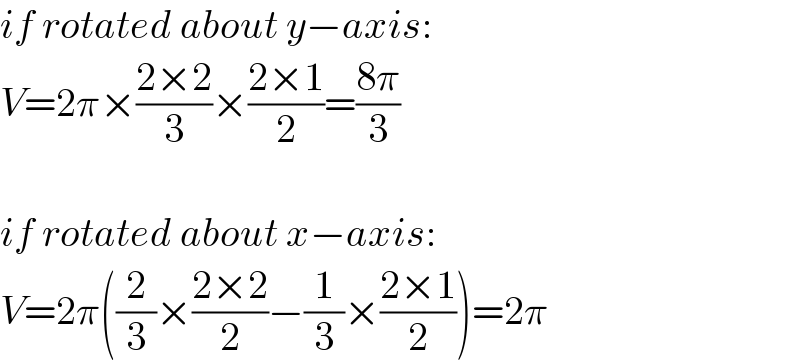
$${if}\:{rotated}\:{about}\:{y}−{axis}: \\ $$$${V}=\mathrm{2}\pi×\frac{\mathrm{2}×\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{2}×\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{8}\pi}{\mathrm{3}} \\ $$$$ \\ $$$${if}\:{rotated}\:{about}\:{x}−{axis}: \\ $$$${V}=\mathrm{2}\pi\left(\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{2}×\mathrm{2}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{2}×\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\pi \\ $$
Commented by universe last updated on 02/Jan/25
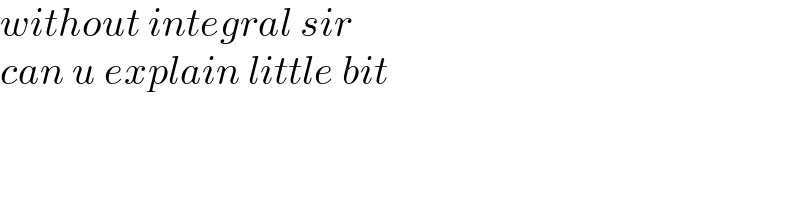
$${without}\:{integral}\:{sir}\: \\ $$$${can}\:{u}\:{explain}\:{little}\:{bit} \\ $$
Commented by mr W last updated on 02/Jan/25
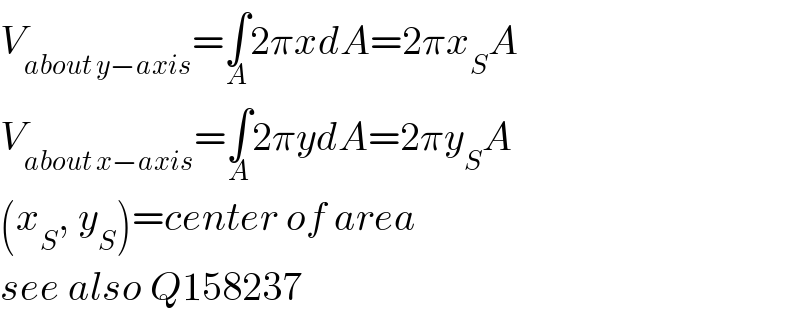
$${V}_{{about}\:{y}−{axis}} =\underset{{A}} {\int}\mathrm{2}\pi{xdA}=\mathrm{2}\pi{x}_{{S}} {A} \\ $$$${V}_{{about}\:{x}−{axis}} =\underset{{A}} {\int}\mathrm{2}\pi{ydA}=\mathrm{2}\pi{y}_{{S}} {A} \\ $$$$\left({x}_{{S}} ,\:{y}_{{S}} \right)={center}\:{of}\:{area} \\ $$$${see}\:{also}\:{Q}\mathrm{158237} \\ $$
Commented by universe last updated on 02/Jan/25

$${thanks} \\ $$
