Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 211749 by universe last updated on 19/Sep/24

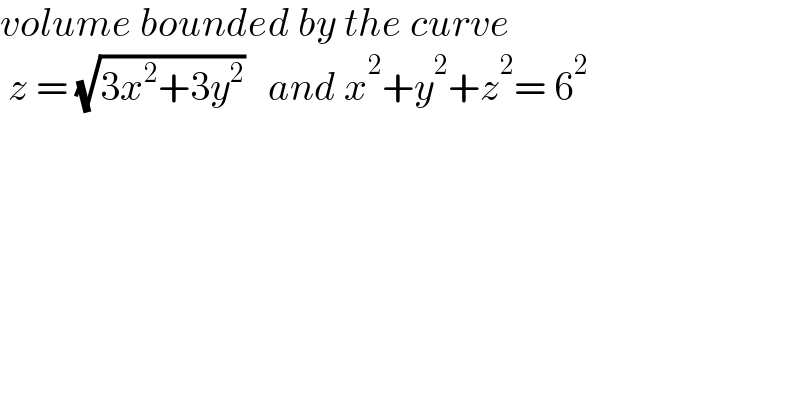
volume bounded by the curve z = (√(3x^2 +3y^2 )) and x^2 +y^2 +z^2 = 6^2

$${volume}\:{bounded}\:{by}\:{the}\:{curve} \\ $$$$\:{z}\:=\:\sqrt{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }\:\:\:{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\:\mathrm{6}^{\mathrm{2}} \\ $$

Answered by mr W last updated on 20/Sep/24

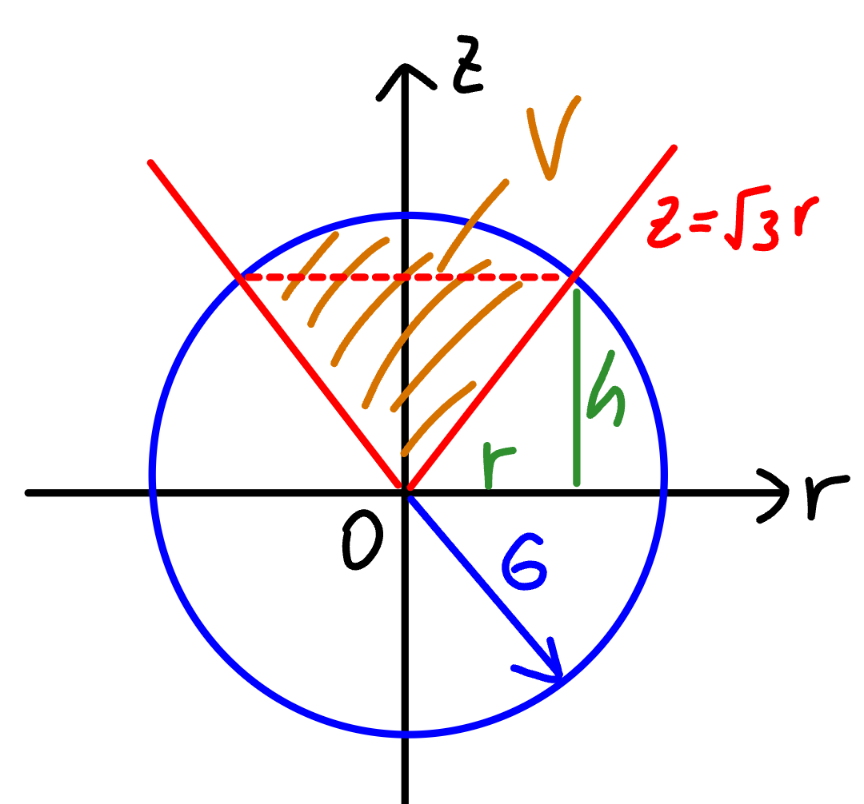
Commented by mr W last updated on 20/Sep/24

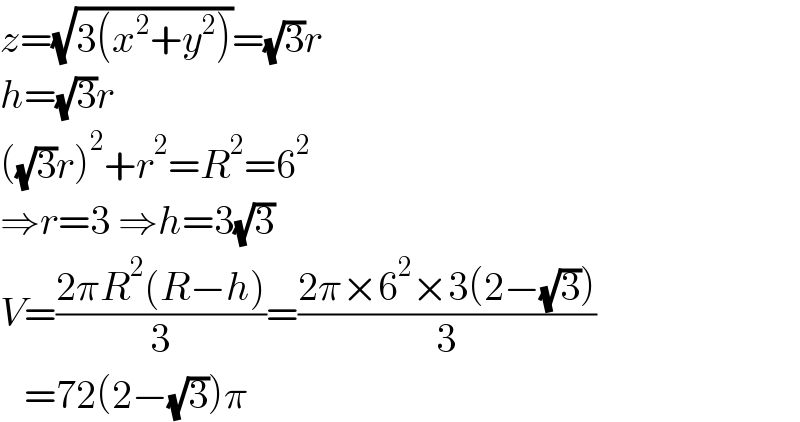
z=(√(3(x^2 +y^2 )))=(√3)r h=(√3)r ((√3)r)^2 +r^2 =R^2 =6^2 ⇒r=3 ⇒h=3(√3) V=((2πR^2 (R−h))/3)=((2π×6^2 ×3(2−(√3)))/3) =72(2−(√3))π

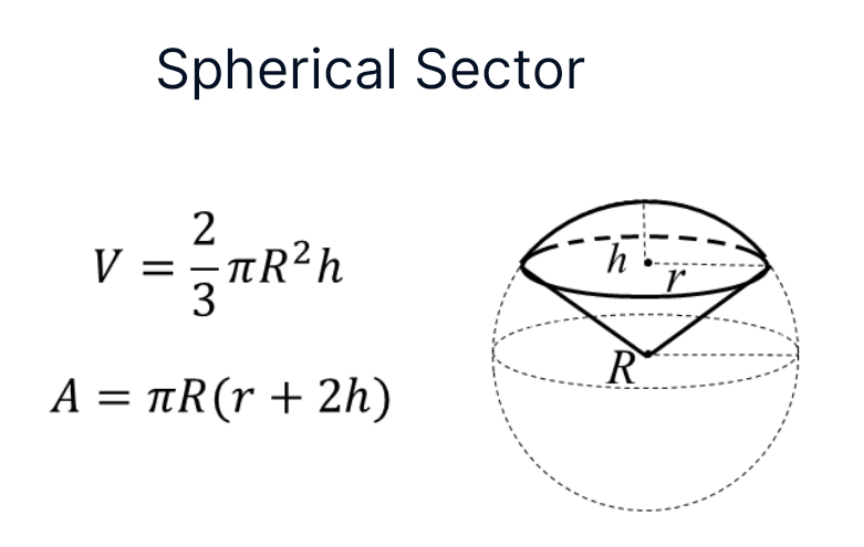
$${z}=\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}=\sqrt{\mathrm{3}}{r} \\ $$$${h}=\sqrt{\mathrm{3}}{r} \\ $$$$\left(\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} ={R}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\mathrm{3}\:\Rightarrow{h}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${V}=\frac{\mathrm{2}\pi{R}^{\mathrm{2}} \left({R}−{h}\right)}{\mathrm{3}}=\frac{\mathrm{2}\pi×\mathrm{6}^{\mathrm{2}} ×\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}} \\ $$$$\:\:\:=\mathrm{72}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\pi \\ $$

Commented by universe last updated on 20/Sep/24

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by universe last updated on 20/Sep/24

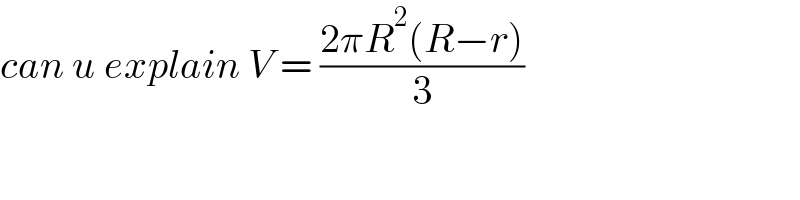
can u explain V = ((2πR^2 (R−r))/3)

$${can}\:{u}\:{explain}\:{V}\:=\:\frac{\mathrm{2}\pi{R}^{\mathrm{2}} \left({R}−{r}\right)}{\mathrm{3}} \\ $$

Commented by mr W last updated on 20/Sep/24

Commented by universe last updated on 20/Sep/24

thanks sir

$${thanks}\:{sir} \\ $$

Answered by BHOOPENDRA last updated on 20/Sep/24

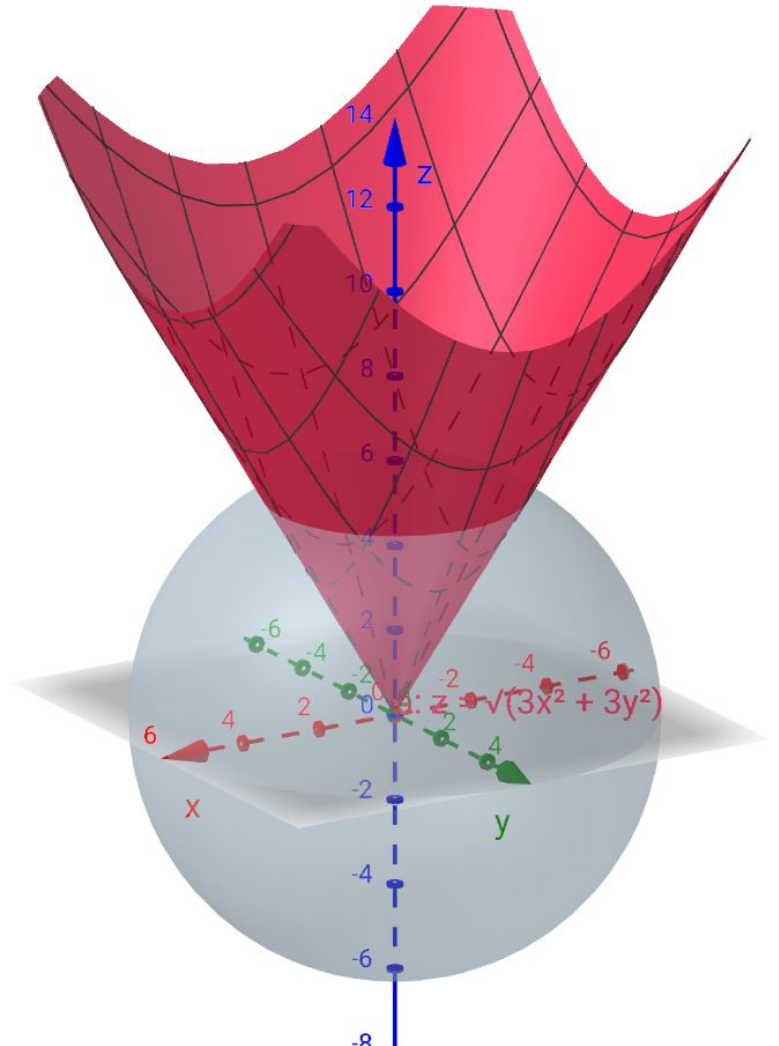
Answered by BHOOPENDRA last updated on 20/Sep/24

V=∫∫∫ ρ^2 sinφ dρ dθ dφ =∫_0 ^(π/6) ∫_0 ^(2π) ∫_0 ^6 ρ^2 sinφ dρ dθ dφ =∫_0 ^(π/6) ∫_0 ^(2π) (((6^3 −0^3 )/3)) sinφ dθ dφ =∫_0 ^(π/6) 72(2π−0)sinφ dφ =−144π cosφ∣_0 ^(π/6) = 144π (((2 −(√3))/2)) =72π (2−(√3))

$${V}=\int\int\int\:\rho^{\mathrm{2}} {sin}\phi\:{d}\rho\:{d}\theta\:{d}\phi \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\int_{\mathrm{0}} ^{\mathrm{6}} \:\rho^{\mathrm{2}} \:{sin}\phi\:{d}\rho\:{d}\theta\:{d}\phi \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\frac{\mathrm{6}^{\mathrm{3}} −\mathrm{0}^{\mathrm{3}} }{\mathrm{3}}\right)\:{sin}\phi\:{d}\theta\:{d}\phi \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{72}\left(\mathrm{2}\pi−\mathrm{0}\right){sin}\phi\:{d}\phi \\ $$$$\:\:\:=−\mathrm{144}\pi\:{cos}\phi\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \\ $$$$\:\:=\:\mathrm{144}\pi\:\left(\frac{\mathrm{2}\:−\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\mathrm{72}\pi\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$

Commented by universe last updated on 20/Sep/24

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by mr W last updated on 20/Sep/24

V=72π(2−(√3)) >0

$${V}=\mathrm{72}\pi\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\:>\mathrm{0} \\ $$

Commented by BHOOPENDRA last updated on 20/Sep/24

Thanks Mr.W it was typo

$${Thanks}\:{Mr}.{W}\:{it}\:{was}\:{typo} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com