
Question Number 128591 by BHOOPENDRA last updated on 09/Jan/21
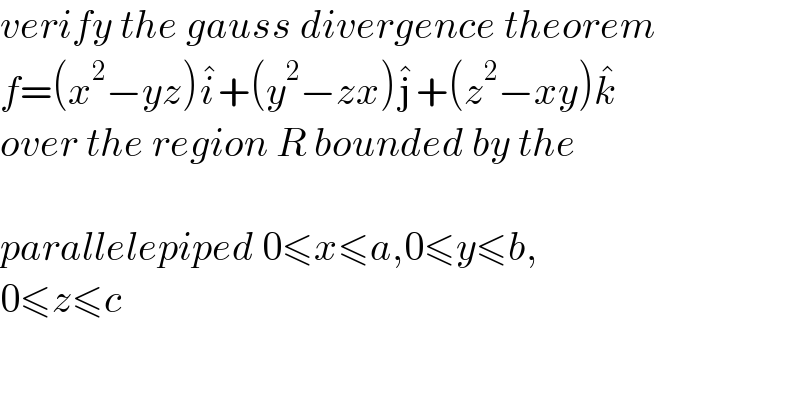
$${verify}\:{the}\:{gauss}\:{divergence}\:{theorem} \\ $$$${f}=\left({x}^{\mathrm{2}} −{yz}\right)\hat {{i}}+\left({y}^{\mathrm{2}} −{zx}\right)\hat {\mathrm{j}}+\left({z}^{\mathrm{2}} −{xy}\right)\hat {{k}} \\ $$$${over}\:{the}\:{region}\:{R}\:{bounded}\:{by}\:{the}\: \\ $$$$ \\ $$$${parallelepiped}\:\mathrm{0}\leqslant{x}\leqslant{a},\mathrm{0}\leqslant{y}\leqslant{b}, \\ $$$$\mathrm{0}\leqslant{z}\leqslant{c} \\ $$
Commented by BHOOPENDRA last updated on 09/Jan/21
$${help}\:{me}\:{out}\:{this}? \\ $$
