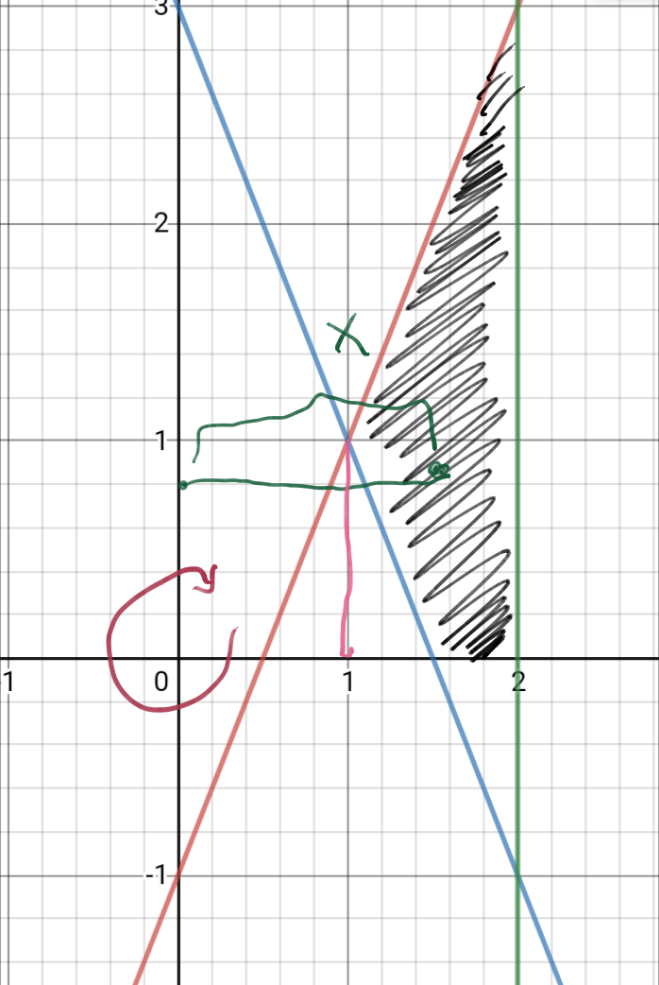
Question Number 95722 by rb222 last updated on 27/May/20

$${use}\:{cylinder}\:{ring}\:{method} \\ $$$$ \\ $$$${y}\:=\:\mathrm{2}{x}−\mathrm{1} \\ $$$${y}\:=\:−\mathrm{2}{x}\:+\:\mathrm{3} \\ $$$${x}\:=\:\mathrm{2}\: \\ $$$$ \\ $$$${y}−{axis}\: \\ $$$$ \\ $$$$ \\ $$
Answered by i jagooll last updated on 27/May/20
![vol = 2π ∫_1 ^2 x(2x−1−(−2x+3))dx = 2π ∫_1 ^2 x(4x−4) dx =2π ∫_1 ^2 (4x^2 −4x) dx =2π [ (4/3)x^3 −2x^2 ]_1 ^2 =2π [ (4/3)(7)−2(3) ] =2π (((28−18)/3)) = ((20π)/3)](Q95728.png)
$$\mathrm{vol}\:=\:\mathrm{2}\pi\:\overset{\mathrm{2}} {\int}_{\mathrm{1}} {x}\left(\mathrm{2}{x}−\mathrm{1}−\left(−\mathrm{2}{x}+\mathrm{3}\right)\right){dx} \\ $$$$=\:\mathrm{2}\pi\:\overset{\mathrm{2}} {\int}_{\mathrm{1}} {x}\left(\mathrm{4}{x}−\mathrm{4}\right)\:{dx}\: \\ $$$$=\mathrm{2}\pi\:\overset{\mathrm{2}} {\int}_{\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}\right)\:{dx}\: \\ $$$$=\mathrm{2}\pi\:\left[\:\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}\pi\:\left[\:\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{7}\right)−\mathrm{2}\left(\mathrm{3}\right)\:\right] \\ $$$$=\mathrm{2}\pi\:\left(\frac{\mathrm{28}−\mathrm{18}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{20}\pi}{\mathrm{3}}\: \\ $$
Commented by rb222 last updated on 27/May/20

$${thanks}\:{sir} \\ $$
Answered by john santu last updated on 27/May/20