
Question Number 128846 by Ar Brandon last updated on 10/Jan/21
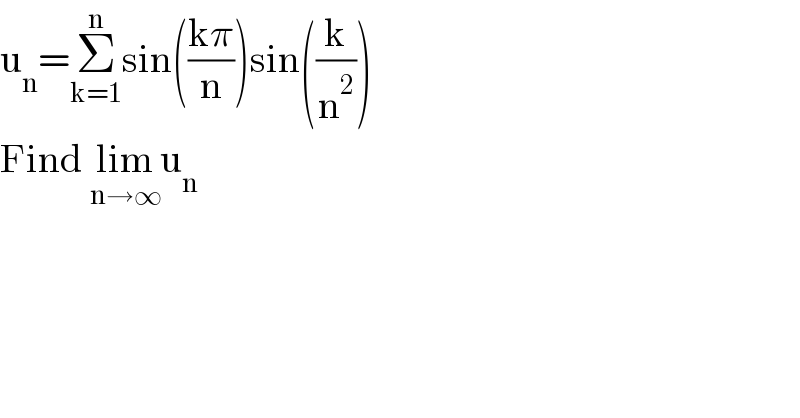
$$\mathrm{u}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{sin}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)\mathrm{sin}\left(\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{Find}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}u}_{\mathrm{n}} \\ $$
Commented by Dwaipayan Shikari last updated on 10/Jan/21
![lim_(n→∞) sin((k/n^2 ))=(k/n^2 ) u_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (k/n)sin((kπ)/n) =∫_0 ^1 xsinxπ dx = (1/π^2 )∫_0 ^π u sinu =(1/π^2 )[−u cosu]_0 ^π +(1/π^2 )∫_0 ^π cosu du =(1/π)](Q128847.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{sin}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right)=\frac{{k}}{{n}^{\mathrm{2}} } \\ $$$${u}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{{n}}{sin}\frac{{k}\pi}{{n}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {xsinx}\pi\:{dx}\:=\:\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} {u}\:{sinu}\:=\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\left[−{u}\:{cosu}\right]_{\mathrm{0}} ^{\pi} +\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} {cosu}\:{du} \\ $$$$=\frac{\mathrm{1}}{\pi} \\ $$
Commented by Dwaipayan Shikari last updated on 10/Jan/21
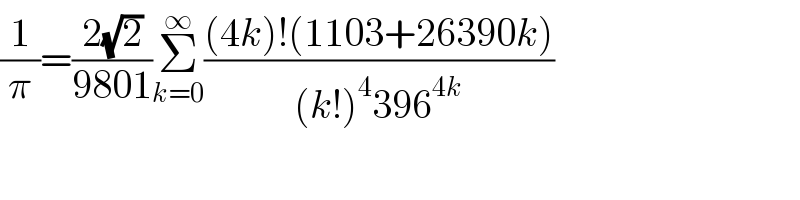
$$\frac{\mathrm{1}}{\pi}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9801}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{4}{k}\right)!\left(\mathrm{1103}+\mathrm{26390}{k}\right)}{\left({k}!\right)^{\mathrm{4}} \mathrm{396}^{\mathrm{4}{k}} } \\ $$
