
Question Number 130782 by EDWIN88 last updated on 28/Jan/21
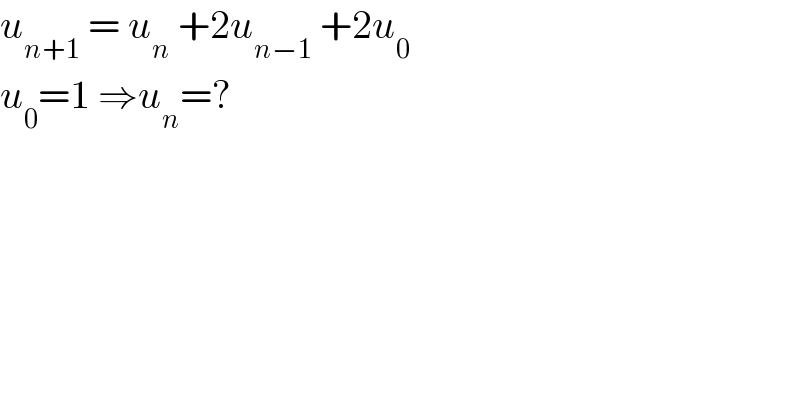
$${u}_{{n}+\mathrm{1}} \:=\:{u}_{{n}} \:+\mathrm{2}{u}_{{n}−\mathrm{1}} \:+\mathrm{2}{u}_{\mathrm{0}} \: \\ $$$${u}_{\mathrm{0}} =\mathrm{1}\:\Rightarrow{u}_{{n}} =? \\ $$
Commented by prakash jain last updated on 29/Jan/21
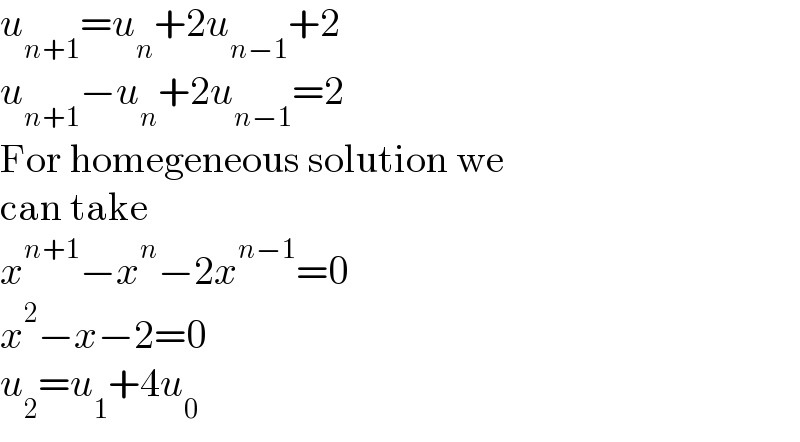
$${u}_{{n}+\mathrm{1}} ={u}_{{n}} +\mathrm{2}{u}_{{n}−\mathrm{1}} +\mathrm{2} \\ $$$${u}_{{n}+\mathrm{1}} −{u}_{{n}} +\mathrm{2}{u}_{{n}−\mathrm{1}} =\mathrm{2} \\ $$$$\mathrm{For}\:\mathrm{homegeneous}\:\mathrm{solution}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{take} \\ $$$${x}^{{n}+\mathrm{1}} −{x}^{{n}} −\mathrm{2}{x}^{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$${u}_{\mathrm{2}} ={u}_{\mathrm{1}} +\mathrm{4}{u}_{\mathrm{0}} \\ $$
Commented by prakash jain last updated on 29/Jan/21

$${u}_{{n}+\mathrm{1}} ={u}_{{n}} +\mathrm{2}{u}_{{n}−\mathrm{1}} +\mathrm{2} \\ $$$${u}_{{n}+\mathrm{1}} −{u}_{\mathrm{2}} −\mathrm{2}{u}_{{n}−\mathrm{1}} =\mathrm{2} \\ $$$$\mathrm{Homigenous}\:\mathrm{solution} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0}\Rightarrow{x}=−\mathrm{1},\mathrm{2} \\ $$$${u}_{{n}} ={c}_{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} +{c}_{\mathrm{2}} \mathrm{2}^{{n}} \\ $$$$\mathrm{General}\:\mathrm{Solution} \\ $$$${u}_{{n}} ={c}_{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} +{c}_{\mathrm{2}} \mathrm{2}^{{n}} −\mathrm{1} \\ $$$$\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{know}\:\mathrm{at}\:\mathrm{least}\:\mathrm{two} \\ $$$$\mathrm{values}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{sequence} \\ $$
Commented by EDWIN88 last updated on 29/Jan/21

$${thank}\:{you} \\ $$
Answered by mr W last updated on 29/Jan/21
![say u_1 =2, u_0 =1 u_(n+1) =u_n +2u_(n−1) +2 let u_n =a_n +c a_(n+1) +c=a_n +c+2(a_(n−1) +c)+2 a_(n+1) =a_n +2a_(n−1) +2c+2 let 2c+2=0, i.e. c=−1 ⇒u_n =a_n −1 ⇒a_(n+1) −a_n −2a_(n−1) =0 x^2 −x−2=0 (x+1)(x−2)=0 ⇒x=−1, 2 a_n =A(−1)^n +B2^n a_0 =A+B=u_0 +1=1+1=2 a_1 =−A+2B=u_1 +1=2+1=3 ⇒B=(5/3), A=(1/3) ⇒u_n =(1/3)[5×2^n +(−1)^n ]−1](Q130803.png)
$${say}\:{u}_{\mathrm{1}} =\mathrm{2},\:{u}_{\mathrm{0}} =\mathrm{1} \\ $$$${u}_{{n}+\mathrm{1}} ={u}_{{n}} +\mathrm{2}{u}_{{n}−\mathrm{1}} +\mathrm{2} \\ $$$${let}\:{u}_{{n}} ={a}_{{n}} +{c} \\ $$$${a}_{{n}+\mathrm{1}} +{c}={a}_{{n}} +{c}+\mathrm{2}\left({a}_{{n}−\mathrm{1}} +{c}\right)+\mathrm{2} \\ $$$${a}_{{n}+\mathrm{1}} ={a}_{{n}} +\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{2}{c}+\mathrm{2} \\ $$$${let}\:\mathrm{2}{c}+\mathrm{2}=\mathrm{0},\:{i}.{e}.\:{c}=−\mathrm{1} \\ $$$$\Rightarrow{u}_{{n}} ={a}_{{n}} −\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}+\mathrm{1}} −{a}_{{n}} −\mathrm{2}{a}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1},\:\mathrm{2} \\ $$$${a}_{{n}} ={A}\left(−\mathrm{1}\right)^{{n}} +{B}\mathrm{2}^{{n}} \\ $$$${a}_{\mathrm{0}} ={A}+{B}={u}_{\mathrm{0}} +\mathrm{1}=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$${a}_{\mathrm{1}} =−{A}+\mathrm{2}{B}={u}_{\mathrm{1}} +\mathrm{1}=\mathrm{2}+\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow{B}=\frac{\mathrm{5}}{\mathrm{3}},\:{A}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{5}×\mathrm{2}^{{n}} +\left(−\mathrm{1}\right)^{{n}} \right]−\mathrm{1} \\ $$
Commented by EDWIN88 last updated on 29/Jan/21

$${thank}\:{you} \\ $$
