
Question Number 130214 by Lordose last updated on 23/Jan/21
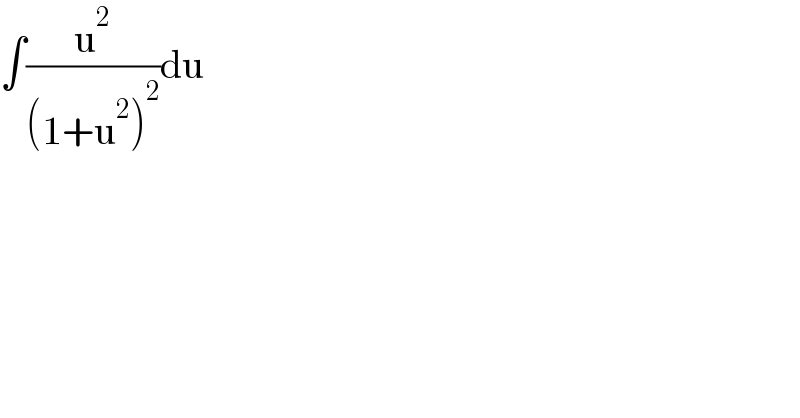
$$\int\frac{\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{du} \\ $$
Answered by liberty last updated on 23/Jan/21
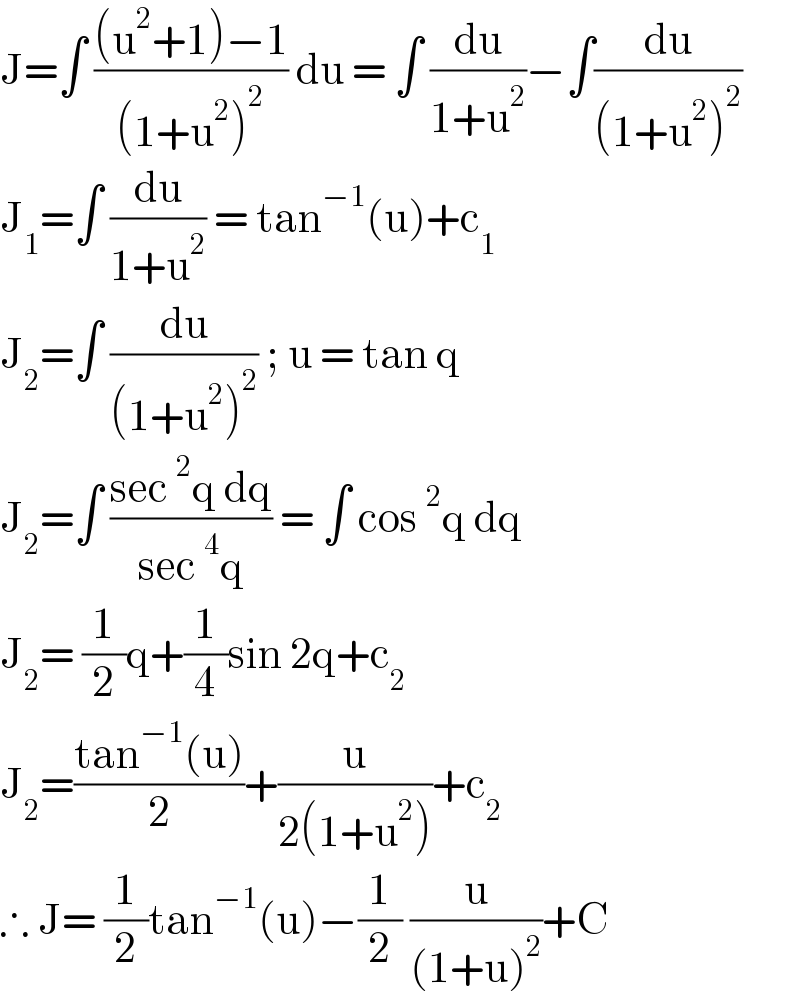
$$\mathrm{J}=\int\:\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\mathrm{du}\:=\:\int\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }−\int\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{J}_{\mathrm{1}} =\int\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)+\mathrm{c}_{\mathrm{1}} \\ $$$$\mathrm{J}_{\mathrm{2}} =\int\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\:;\:\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{q} \\ $$$$\mathrm{J}_{\mathrm{2}} =\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{q}\:\mathrm{dq}}{\mathrm{sec}\:^{\mathrm{4}} \mathrm{q}}\:=\:\int\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}\:\mathrm{dq} \\ $$$$\mathrm{J}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{q}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2q}+\mathrm{c}_{\mathrm{2}} \\ $$$$\mathrm{J}_{\mathrm{2}} =\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)}{\mathrm{2}}+\frac{\mathrm{u}}{\mathrm{2}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}+\mathrm{c}_{\mathrm{2}} \\ $$$$\therefore\:\mathrm{J}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{u}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }+\mathrm{C} \\ $$
