
Question Number 199709 by tri26112004 last updated on 08/Nov/23
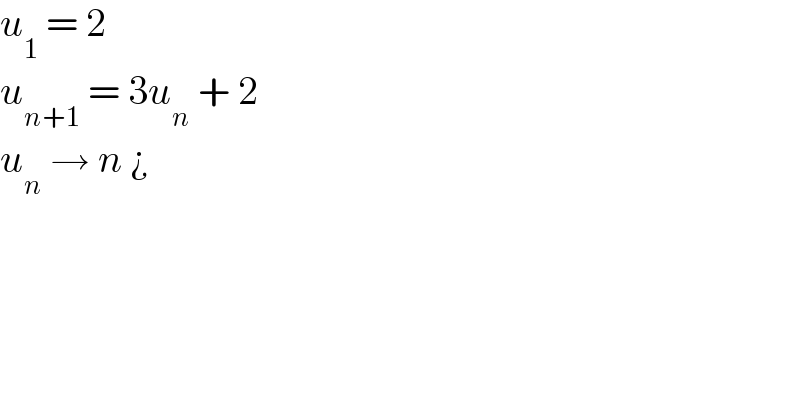
$${u}_{\mathrm{1}} \:=\:\mathrm{2}\: \\ $$$${u}_{{n}+\mathrm{1}} \:=\:\mathrm{3}{u}_{{n}} \:+\:\mathrm{2} \\ $$$${u}_{{n}} \:\rightarrow\:{n}\:¿ \\ $$
Answered by mr W last updated on 08/Nov/23
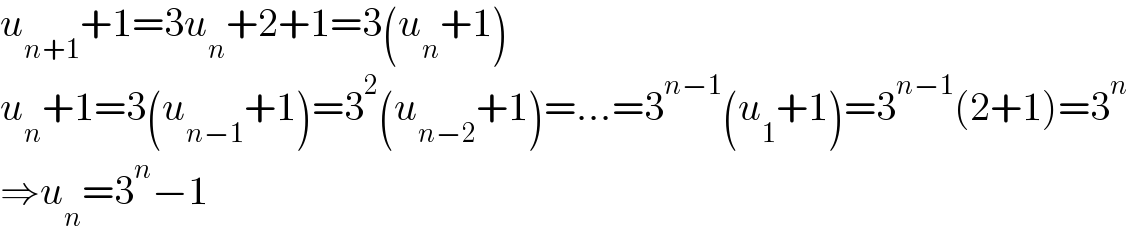
$${u}_{{n}+\mathrm{1}} +\mathrm{1}=\mathrm{3}{u}_{{n}} +\mathrm{2}+\mathrm{1}=\mathrm{3}\left({u}_{{n}} +\mathrm{1}\right) \\ $$$${u}_{{n}} +\mathrm{1}=\mathrm{3}\left({u}_{{n}−\mathrm{1}} +\mathrm{1}\right)=\mathrm{3}^{\mathrm{2}} \left({u}_{{n}−\mathrm{2}} +\mathrm{1}\right)=...=\mathrm{3}^{{n}−\mathrm{1}} \left({u}_{\mathrm{1}} +\mathrm{1}\right)=\mathrm{3}^{{n}−\mathrm{1}} \left(\mathrm{2}+\mathrm{1}\right)=\mathrm{3}^{{n}} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{3}^{{n}} −\mathrm{1} \\ $$
