
Question Number 47331 by MJS last updated on 08/Nov/18
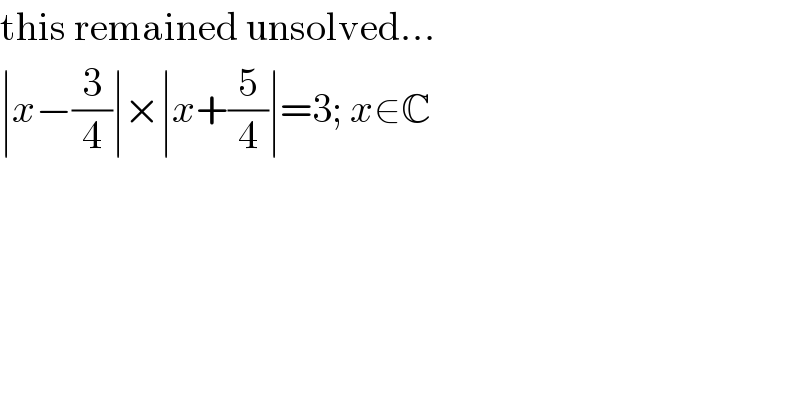
$$\mathrm{this}\:\mathrm{remained}\:\mathrm{unsolved}... \\ $$$$\mid{x}−\frac{\mathrm{3}}{\mathrm{4}}\mid×\mid{x}+\frac{\mathrm{5}}{\mathrm{4}}\mid=\mathrm{3};\:{x}\in\mathbb{C} \\ $$
Commented by MJS last updated on 08/Nov/18

$$\mid{a}−\frac{\mathrm{3}}{\mathrm{4}}+{b}\mathrm{i}\mid×\mid{a}+\frac{\mathrm{5}}{\mathrm{4}}+{b}\mathrm{i}\mid=\mathrm{3}\:\mathrm{with}\:{a},\:{b}\:\in\mathbb{R} \\ $$$$\sqrt{\left({a}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }\sqrt{\left({a}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{3} \\ $$$${b}^{\mathrm{4}} +\left(\mathrm{2}{a}^{\mathrm{2}} +{a}+\frac{\mathrm{17}}{\mathrm{8}}\right){b}^{\mathrm{2}} +\left({a}^{\mathrm{4}} +{a}^{\mathrm{3}} −\frac{\mathrm{13}}{\mathrm{8}}{a}^{\mathrm{2}} −\frac{\mathrm{15}}{\mathrm{16}}{a}−\frac{\mathrm{2079}}{\mathrm{256}}\right)=\mathrm{0} \\ $$$${b}^{\mathrm{2}} =−{a}^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}−\frac{\mathrm{17}}{\mathrm{16}}\pm\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\frac{\mathrm{37}}{\mathrm{4}}} \\ $$$${b}\in\mathbb{R}\:\Rightarrow\:{b}=\pm\sqrt{−{a}^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}−\frac{\mathrm{17}}{\mathrm{16}}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\frac{\mathrm{37}}{\mathrm{4}}}} \\ $$$$\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\frac{\mathrm{37}}{\mathrm{4}}}\geqslant{a}^{\mathrm{2}} +\frac{{a}}{\mathrm{2}}+\frac{\mathrm{17}}{\mathrm{16}}\:\Rightarrow\:−\frac{\mathrm{9}}{\mathrm{4}}\leqslant{a}\leqslant\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{solution}\:\mathrm{is} \\ $$$${x}={a}\pm\mathrm{i}\sqrt{−{a}^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}−\frac{\mathrm{17}}{\mathrm{16}}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\frac{\mathrm{37}}{\mathrm{4}}}}\:\mathrm{with}\:−\frac{\mathrm{9}}{\mathrm{4}}\leqslant{a}\leqslant\frac{\mathrm{7}}{\mathrm{4}} \\ $$
