Question Number 196221 by liuxinnan last updated on 20/Aug/23

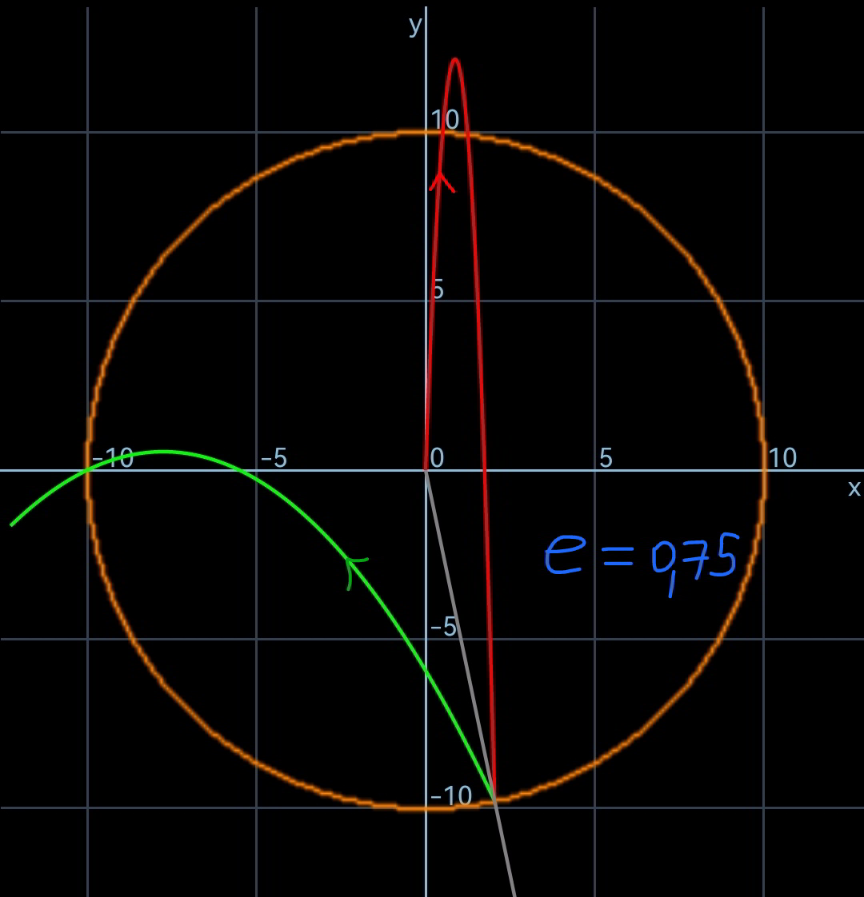
$${there}\:{is}\:{a}\:{cylinder}\:{on}\:{the}\:{horizontal}\:{plane} \\ $$$${and}\:{there}\:{is}\:{a}\:{little}\:{ball}\:{with}\:{mass}\:{m} \\ $$$${at}\:{the}\:{center}\:{of}\:{a}\:{circle}\:{on}\:{the}\:{vertical}\:{plane} \\ $$$${and}\:{there}\:{is}\:{a}\:{little}\:{hole}\:{in}\:{the}\:{wall}\:{of} \\ $$$${the}\:{cylinder}\:{on}\:{the}\:{lift}\:{of}\:{the}\:{ball}\:{which} \\ $$$${just}\:{enough}\:{for}\:{the}\:{ball}\:{to}\:{pass}\:{through} \\ $$$${the}\:{gravitational}\:{acceleration}\:{is}\:{g} \\ $$$${the}\:{collision}\:{between}\:{the}\:{ball}\:{and} \\ $$$${the}\:{cylinder}\:{wall}\:{can}\:{be}\:{regarded}\:{as} \\ $$$${an}\:{elastic}\:{coollision} \\ $$$${find}\:{all}\:{of}\:{the}\:{quondam}\:{speed} \\ $$
Commented by liuxinnan last updated on 20/Aug/23
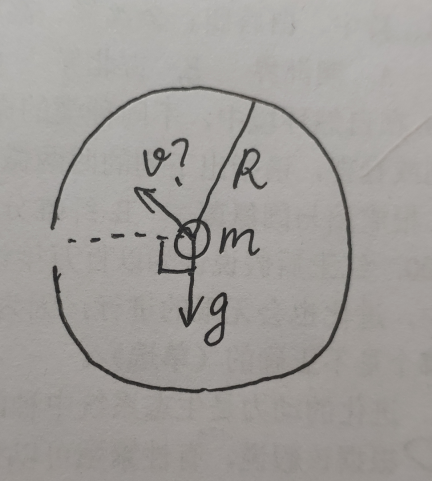
Commented by mr W last updated on 20/Aug/23

$${there}\:{are}\:{many}\:{possibilities}. \\ $$$${do}\:{you}\:{mean}\:{that}\:{the}\:{ball}\:{should}\:{fly} \\ $$$${through}\:{the}\:{hole}\:{just}\:{after}\:{one}\:{time}\: \\ $$$${collision}\:{with}\:{the}\:{cylinder}\:{wall}? \\ $$$${the}\:{ball}\:{can}\:{also}\:{directly}\:{fly}\:{through} \\ $$$${the}\:{hole}\:{without}\:{collision}\:{or}\:{after} \\ $$$${two}\:{times}\:{collision}\:{etc}. \\ $$
Commented by liuxinnan last updated on 20/Aug/23
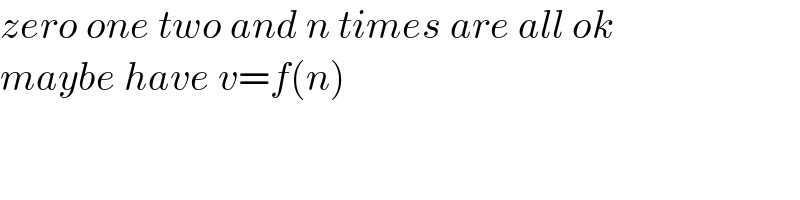
$${zero}\:{one}\:{two}\:{and}\:{n}\:{times}\:{are}\:{all}\:{ok} \\ $$$${maybe}\:{have}\:{v}={f}\left({n}\right) \\ $$
Answered by mr W last updated on 21/Aug/23
Commented by mr W last updated on 23/Aug/23

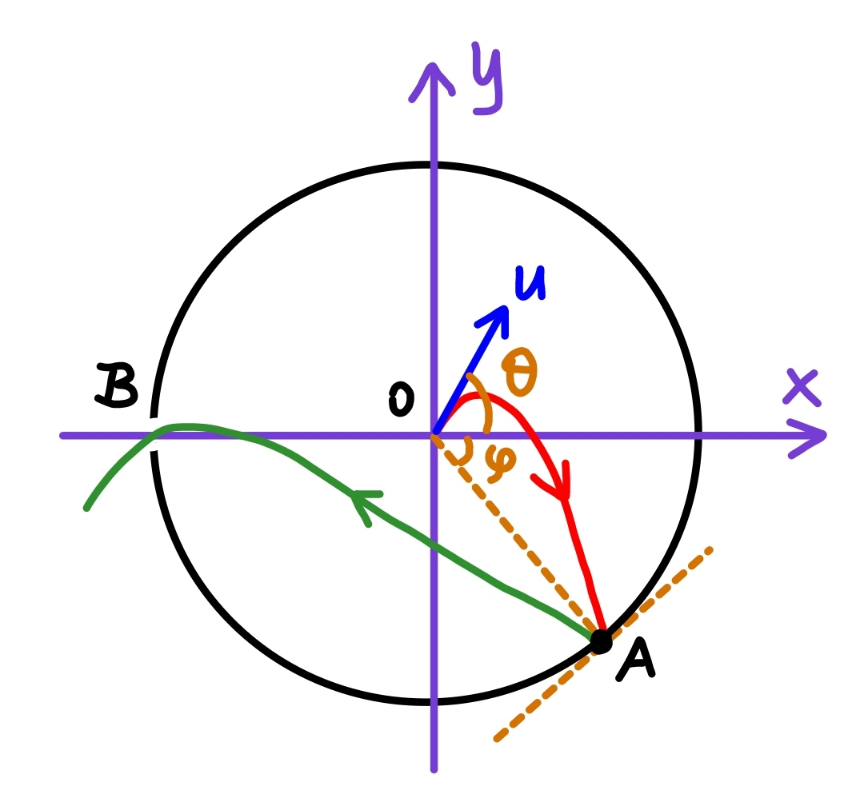
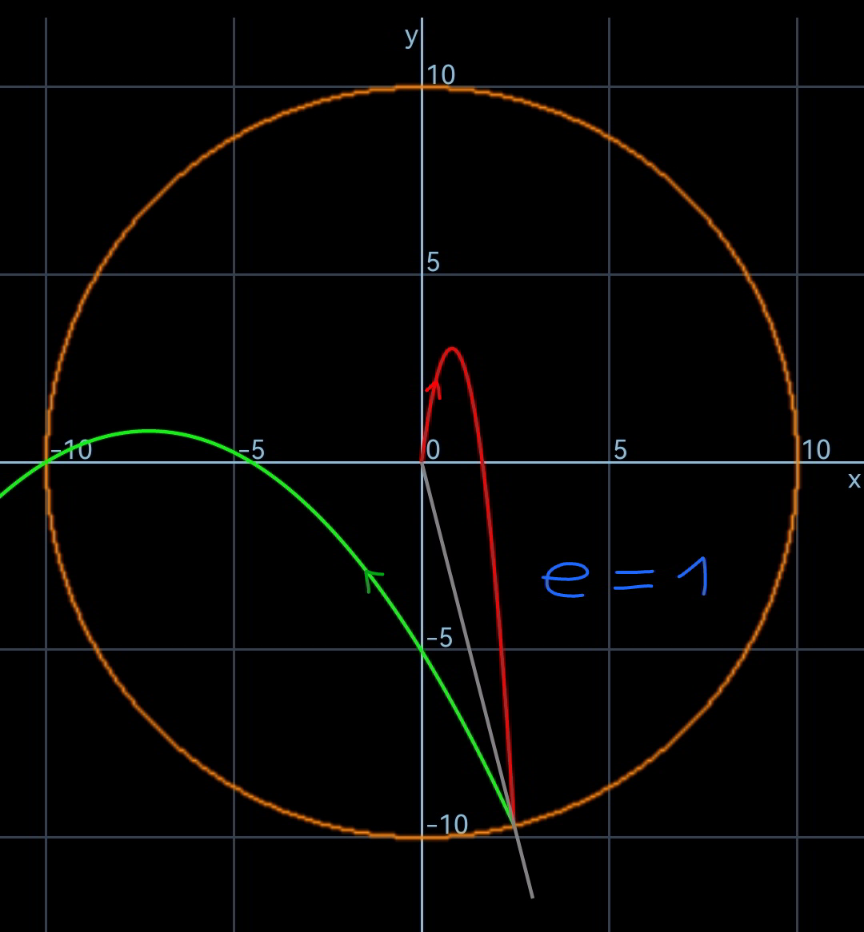
$${let}'{s}\:{consider}\:{the}\:{case}\:{that}\:{the} \\ $$$${ball}\:{flys}\:{through}\:{the}\:{hole}\:{after}\:{a} \\ $$$${single}\:{collision}\:{with}\:{the}\:{cylinder} \\ $$$${wall}. \\ $$
Commented by mr W last updated on 22/Aug/23
Commented by mr W last updated on 23/Aug/23
![from O to A: t=((R cos ϕ)/(u cos θ)) −R sin ϕ=u sin θ ×((R cos ϕ)/(u cos θ))−(g/2)×(((R cos ϕ)/(u cos θ)))^2 −tan ϕ=tan θ −((gR cos ϕ (1+tan^2 θ))/(2u^2 )) let λ=((gR)/(2u^2 )) tan ϕ+tan θ =λ cos ϕ (1+tan^2 θ) λ cos ϕ tan^2 θ−tan θ−tan ϕ+λ cos ϕ=0 ⇒tan θ=((1+(√(1+4λ(sin ϕ−λ cos^2 ϕ))))/(2λ cos ϕ)) at A: U_x =u cos θ U_y =u sin θ−g×((R cos ϕ)/(u cos θ)) =u(sin θ−((2λ cos ϕ)/(cos θ))) =u cos θ[tan θ−2λ cos ϕ (1+tan^2 θ)] V_x =[(1+e)sin^2 ϕ−1]u cos θ−(1+e)sin ϕ cos ϕ u(sin θ−((2λ cos ϕ)/(cos θ))) =u cos θ {(1+e) sin^2 ϕ−1−(1+e)sin ϕ cos ϕ[tan θ−2λ cos ϕ (1+tan^2 θ)]} V_y =(1+e)sin ϕ cos ϕ u cos θ−[(1+e)cos^2 ϕ−1]u cos θ[tan θ−2λ cos ϕ (1+tan^2 θ)] =u cos θ {(1+e)sin ϕ cos ϕ−[(1+e) cos^2 ϕ−1][tan θ−2λ cos ϕ (1+tan^2 θ)]} from A to B: t=((ξR)/u) ξ=(((1+cos ϕ))/(cos θ {(1+e) sin^2 ϕ−1−(1+e)sin ϕ cos ϕ[tan θ−2λ cos ϕ (1+tan^2 θ)]})) R sin ϕ=u cos θ {(1+e)sin ϕ cos ϕ−(e cos^2 ϕ−sin^2 ϕ)[tan θ−2λ cos ϕ (1+tan^2 θ)]}t−((gt^2 )/2) sin ϕ=cos θ {(1+e)sin ϕ cos ϕ−[(1+e) cos^2 ϕ−1][tan θ−2λ cos ϕ (1+tan^2 θ)]}ξ−λξ^2 for a given e we find a λ_(max) such that this equation has one and only one root for 0<ϕ<(π/2). u_(min) =(√((gR)/(2λ_(max) ))) for e=1: u_(min) ≈((√(gR))/(1.274))](Q196339.png)
$${from}\:{O}\:{to}\:{A}: \\ $$$${t}=\frac{{R}\:\mathrm{cos}\:\varphi}{{u}\:\mathrm{cos}\:\theta} \\ $$$$−{R}\:\mathrm{sin}\:\varphi={u}\:\mathrm{sin}\:\theta\:×\frac{{R}\:\mathrm{cos}\:\varphi}{{u}\:\mathrm{cos}\:\theta}−\frac{{g}}{\mathrm{2}}×\left(\frac{{R}\:\mathrm{cos}\:\varphi}{{u}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$$−\mathrm{tan}\:\varphi=\mathrm{tan}\:\theta\:−\frac{{gR}\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${let}\:\lambda=\frac{{gR}}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\varphi+\mathrm{tan}\:\theta\:=\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right) \\ $$$$\lambda\:\mathrm{cos}\:\varphi\:\mathrm{tan}^{\mathrm{2}} \:\theta−\mathrm{tan}\:\theta−\mathrm{tan}\:\varphi+\lambda\:\mathrm{cos}\:\varphi=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}\lambda\left(\mathrm{sin}\:\varphi−\lambda\:\mathrm{cos}^{\mathrm{2}} \:\varphi\right)}}{\mathrm{2}\lambda\:\mathrm{cos}\:\varphi} \\ $$$${at}\:{A}: \\ $$$${U}_{{x}} ={u}\:\mathrm{cos}\:\theta \\ $$$${U}_{{y}} ={u}\:\mathrm{sin}\:\theta−{g}×\frac{{R}\:\mathrm{cos}\:\varphi}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:={u}\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\lambda\:\mathrm{cos}\:\varphi}{\mathrm{cos}\:\theta}\right) \\ $$$$\:\:\:\:={u}\:\mathrm{cos}\:\theta\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right] \\ $$$${V}_{{x}} =\left[\left(\mathrm{1}+{e}\right)\mathrm{sin}^{\mathrm{2}} \:\varphi−\mathrm{1}\right]{u}\:\mathrm{cos}\:\theta−\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:{u}\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\lambda\:\mathrm{cos}\:\varphi}{\mathrm{cos}\:\theta}\right) \\ $$$$\:\:\:\:\:={u}\:\mathrm{cos}\:\theta\:\left\{\left(\mathrm{1}+{e}\right)\:\mathrm{sin}^{\mathrm{2}} \:\varphi−\mathrm{1}−\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right]\right\} \\ $$$${V}_{{y}} =\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:{u}\:\mathrm{cos}\:\theta−\left[\left(\mathrm{1}+{e}\right)\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{1}\right]{u}\:\mathrm{cos}\:\theta\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right] \\ $$$$\:\:\:={u}\:\mathrm{cos}\:\theta\:\left\{\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi−\left[\left(\mathrm{1}+{e}\right)\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{1}\right]\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right]\right\} \\ $$$${from}\:{A}\:{to}\:{B}: \\ $$$${t}=\frac{\xi{R}}{{u}} \\ $$$$\xi=\frac{\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}{\mathrm{cos}\:\theta\:\left\{\left(\mathrm{1}+{e}\right)\:\mathrm{sin}^{\mathrm{2}} \:\varphi−\mathrm{1}−\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right]\right\}} \\ $$$${R}\:\mathrm{sin}\:\varphi={u}\:\mathrm{cos}\:\theta\:\left\{\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi−\left({e}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{sin}^{\mathrm{2}} \:\varphi\right)\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right]\right\}{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{sin}\:\varphi=\mathrm{cos}\:\theta\:\left\{\left(\mathrm{1}+{e}\right)\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi−\left[\left(\mathrm{1}+{e}\right)\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{1}\right]\left[\mathrm{tan}\:\theta−\mathrm{2}\lambda\:\mathrm{cos}\:\varphi\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right]\right\}\xi−\lambda\xi^{\mathrm{2}} \\ $$$${for}\:{a}\:{given}\:{e}\:{we}\:{find}\:{a}\:\lambda_{{max}} \:{such}\:{that} \\ $$$${this}\:{equation}\:{has}\:{one}\:{and}\:{only}\:{one}\: \\ $$$${root}\:{for}\:\mathrm{0}<\varphi<\frac{\pi}{\mathrm{2}}. \\ $$$${u}_{{min}} =\sqrt{\frac{{gR}}{\mathrm{2}\lambda_{{max}} }} \\ $$$${for}\:{e}=\mathrm{1}:\:{u}_{{min}} \approx\frac{\sqrt{{gR}}}{\mathrm{1}.\mathrm{274}} \\ $$
Commented by mr W last updated on 22/Aug/23