
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 180585 by mr W last updated on 14/Nov/22

$${there}\:{are}\:\mathrm{5}\:{points}\:{on}\:{a}\:{line}\:{and}\:\mathrm{4}\: \\ $$$${points}\:{on}\:{a}\:{parallel}\:{line}. \\ $$$${how}\:{many}\:{quadrilaterals}\:{can}\:{be}\: \\ $$$${formed}\:{with}\:{these}\:{points}\:{as}\: \\ $$$${vertrices}? \\ $$
Answered by nikif99 last updated on 14/Nov/22
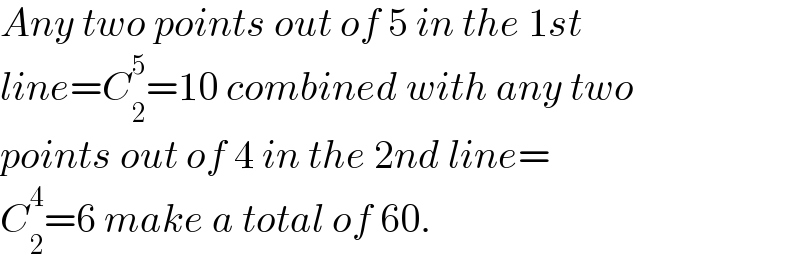
$${Any}\:{two}\:{points}\:{out}\:{of}\:\mathrm{5}\:{in}\:{the}\:\mathrm{1}{st} \\ $$$${line}={C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{10}\:{combined}\:{with}\:{any}\:{two} \\ $$$${points}\:{out}\:{of}\:\mathrm{4}\:{in}\:{the}\:\mathrm{2}{nd}\:{line}= \\ $$$${C}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{6}\:{make}\:{a}\:{total}\:{of}\:\mathrm{60}. \\ $$
Commented by mr W last updated on 14/Nov/22
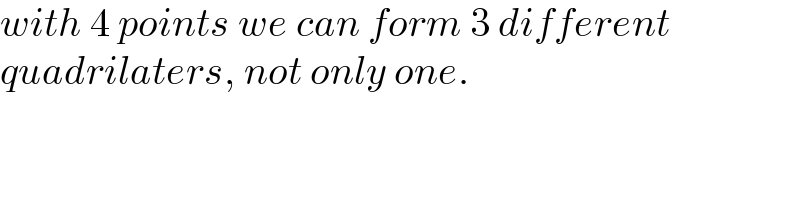
$${with}\:\mathrm{4}\:{points}\:{we}\:{can}\:{form}\:\mathrm{3}\:{different} \\ $$$${quadrilaters},\:{not}\:{only}\:{one}. \\ $$
Commented by nikif99 last updated on 14/Nov/22

$${If}\:{I}\:{well}\:{understood}\:{your}\:{comment}\:{Sir}, \\ $$$${you}\:{mean}\:{there}\:{are}\:\mathrm{3}\:{possible} \\ $$$${quadrilaters}\:{having}\:\mathrm{2}\:{vertices}\:{in}\: \\ $$$${any}\:\mathrm{4}\:{points}\:{of}\:{a}\:{line}? \\ $$
Commented by nikif99 last updated on 14/Nov/22

Commented by mr W last updated on 14/Nov/22

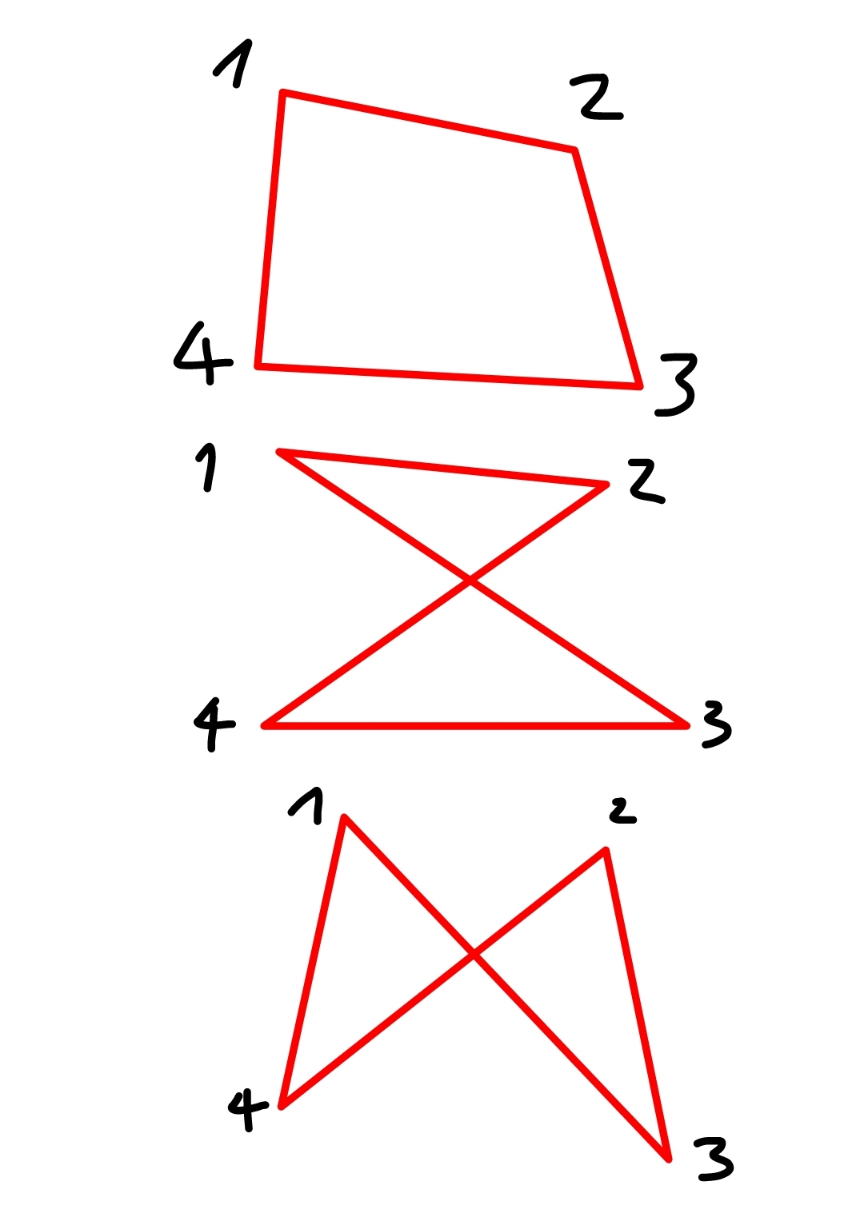
$${i}\:{mean}:\:{when}\:{we}\:{have}\:\mathrm{4}\:{points},\:{we}\:{can} \\ $$$${form}\:\mathrm{3}\:{different}\:{quadrilaterals}, \\ $$$${see}\:{example}\:{below}. \\ $$$${so}\:{tatally}\:\mathrm{60}×\mathrm{3}=\mathrm{180}\:{quadrilaterals} \\ $$$${can}\:{be}\:{formed}. \\ $$
Commented by mr W last updated on 14/Nov/22
Commented by nikif99 last updated on 14/Nov/22
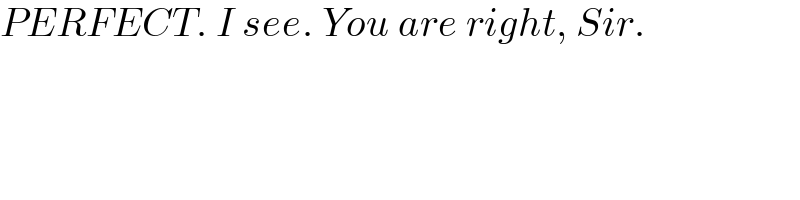
$${PERFECT}.\:{I}\:{see}.\:{You}\:{are}\:{right},\:{Sir}. \\ $$
Answered by cortano1 last updated on 14/Nov/22

$$\begin{pmatrix}{\mathrm{9}}\\{\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{5}}\\{\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{4}}\\{\mathrm{4}}\end{pmatrix}\: \\ $$$$=\:\frac{\mathrm{9}.\mathrm{8}.\mathrm{7}.\mathrm{6}}{\mathrm{4}.\mathrm{3}.\mathrm{2}.\mathrm{1}}\:−\:\mathrm{5}−\mathrm{1} \\ $$$$=\:\mathrm{126}−\mathrm{6}=\mathrm{120}\: \\ $$
