
Question Number 33413 by Rio Mike last updated on 15/Apr/18
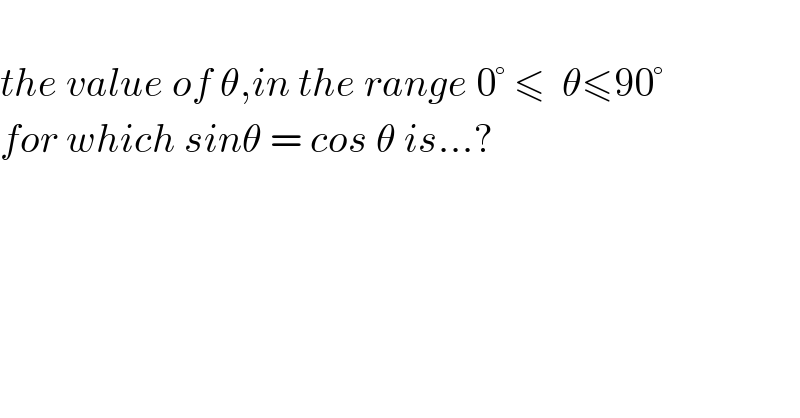
$$ \\ $$$${the}\:{value}\:{of}\:\theta,{in}\:{the}\:{range}\:\mathrm{0}°\:\leqslant\:\:\theta\leqslant\mathrm{90}° \\ $$$${for}\:{which}\:{sin}\theta\:=\:{cos}\:\theta\:{is}...? \\ $$
Commented by Rasheed.Sindhi last updated on 16/Apr/18

$$\mathrm{sin}\theta=\mathrm{cos}\left(\mathrm{90}−\theta\right) \\ $$$$\:\:\:\theta=\mathrm{90}−\theta \\ $$$$\:\:\:\mathrm{2}\theta=\mathrm{90} \\ $$$$\:\:\:\:\theta=\mathrm{45} \\ $$$$\mathrm{sin45}=\mathrm{cos45} \\ $$$$ \\ $$
Commented by abdo imad last updated on 17/Apr/18
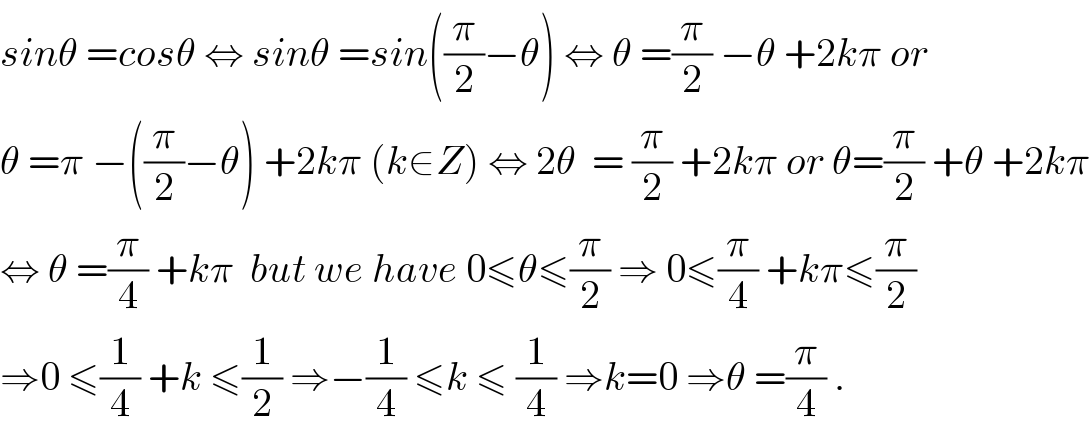
$${sin}\theta\:={cos}\theta\:\Leftrightarrow\:{sin}\theta\:={sin}\left(\frac{\pi}{\mathrm{2}}−\theta\right)\:\Leftrightarrow\:\theta\:=\frac{\pi}{\mathrm{2}}\:−\theta\:+\mathrm{2}{k}\pi\:{or} \\ $$$$\theta\:=\pi\:−\left(\frac{\pi}{\mathrm{2}}−\theta\right)\:+\mathrm{2}{k}\pi\:\left({k}\in{Z}\right)\:\Leftrightarrow\:\mathrm{2}\theta\:\:=\:\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:{or}\:\theta=\frac{\pi}{\mathrm{2}}\:+\theta\:+\mathrm{2}{k}\pi \\ $$$$\Leftrightarrow\:\theta\:=\frac{\pi}{\mathrm{4}}\:+{k}\pi\:\:{but}\:{we}\:{have}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{0}\leqslant\frac{\pi}{\mathrm{4}}\:+{k}\pi\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{0}\:\leqslant\frac{\mathrm{1}}{\mathrm{4}}\:+{k}\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow−\frac{\mathrm{1}}{\mathrm{4}}\:\leqslant{k}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{k}=\mathrm{0}\:\Rightarrow\theta\:=\frac{\pi}{\mathrm{4}}\:. \\ $$
