Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 188758 by Humble last updated on 06/Mar/23

the sum of the first three terms of an AP is 21 and the sum of the first five terms is 55. find. (1) the first term (2) common difference (3) the sum of the first ten term of the sequence

$${the}\:{sum}\:{of}\:{the}\:\:{first}\:{three}\:{terms} \\ $$$${of}\:{an}\:{AP}\:{is}\:\mathrm{21}\:{and}\:\:{the}\:{sum}\:{of}\:{the} \\ $$$${first}\:\:{five}\:{terms}\:{is}\:\mathrm{55}.\:{find}. \\ $$$$\left(\mathrm{1}\right)\:{the}\:{first}\:{term} \\ $$$$\left(\mathrm{2}\right)\:{common}\:{difference} \\ $$$$\left(\mathrm{3}\right)\:{the}\:{sum}\:{of}\:{the}\:{first}\:{ten}\:{term} \\ $$$${of}\:{the}\:\:{sequence} \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 06/Mar/23

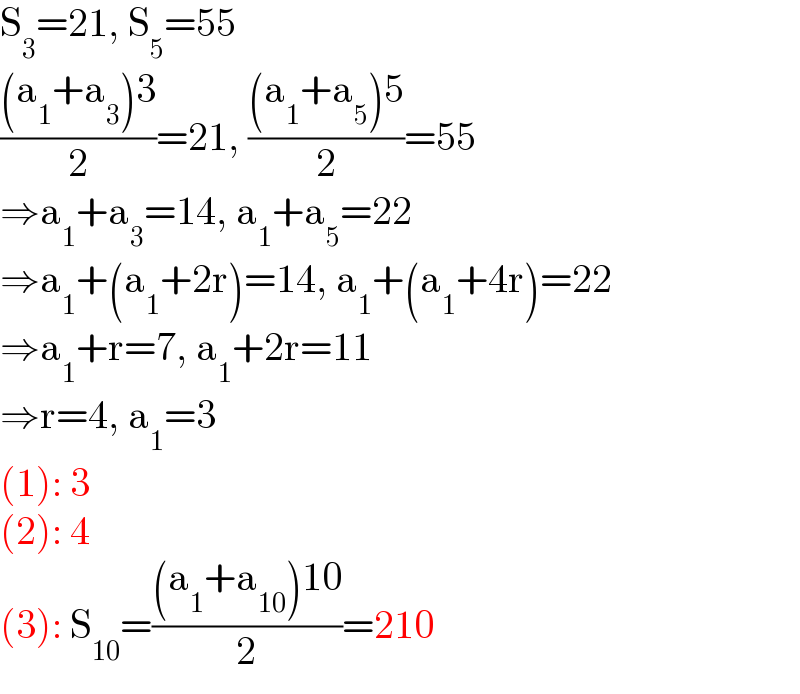
S_3 =21, S_5 =55 (((a_1 +a_3 )3)/2)=21, (((a_1 +a_5 )5)/2)=55 ⇒a_1 +a_3 =14, a_1 +a_5 =22 ⇒a_1 +(a_1 +2r)=14, a_1 +(a_1 +4r)=22 ⇒a_1 +r=7, a_1 +2r=11 ⇒r=4, a_1 =3 (1): 3 (2): 4 (3): S_(10) =(((a_1 +a_(10) )10)/2)=210

$$\mathrm{S}_{\mathrm{3}} =\mathrm{21},\:\mathrm{S}_{\mathrm{5}} =\mathrm{55} \\ $$$$\frac{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{3}} \right)\mathrm{3}}{\mathrm{2}}=\mathrm{21},\:\frac{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{5}} \right)\mathrm{5}}{\mathrm{2}}=\mathrm{55} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{3}} =\mathrm{14},\:\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{5}} =\mathrm{22} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{1}} +\left(\mathrm{a}_{\mathrm{1}} +\mathrm{2r}\right)=\mathrm{14},\:\mathrm{a}_{\mathrm{1}} +\left(\mathrm{a}_{\mathrm{1}} +\mathrm{4r}\right)=\mathrm{22} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{1}} +\mathrm{r}=\mathrm{7},\:\mathrm{a}_{\mathrm{1}} +\mathrm{2r}=\mathrm{11} \\ $$$$\Rightarrow\mathrm{r}=\mathrm{4},\:\mathrm{a}_{\mathrm{1}} =\mathrm{3} \\ $$$$\left(\mathrm{1}\right):\:\mathrm{3} \\ $$$$\left(\mathrm{2}\right):\:\mathrm{4} \\ $$$$\left(\mathrm{3}\right):\:\mathrm{S}_{\mathrm{10}} =\frac{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{10}} \right)\mathrm{10}}{\mathrm{2}}=\mathrm{210} \\ $$

Answered by Rasheed.Sindhi last updated on 06/Mar/23

Let t is third term of the AP (t−2d)+(t−d)+t+(t+d)+(t+2d)=55 5t=55⇒t=11 (t−2d)+(t−d)+t=21 3t−3d=21 3(11)−3d=21⇒d=((33−21)/3)=4 first term=a=t−2d=11−2(4)=3 S_(10) =((10)/2)[2(3)+(10−1)(4)] =5(6+36)=210

$${Let}\:{t}\:{is}\:{third}\:{term}\:{of}\:{the}\:{AP} \\ $$$$\left({t}−\mathrm{2}{d}\right)+\left({t}−{d}\right)+{t}+\left({t}+{d}\right)+\left({t}+\mathrm{2}{d}\right)=\mathrm{55} \\ $$$$\mathrm{5}{t}=\mathrm{55}\Rightarrow{t}=\mathrm{11} \\ $$$$\left({t}−\mathrm{2}{d}\right)+\left({t}−{d}\right)+{t}=\mathrm{21} \\ $$$$\mathrm{3}{t}−\mathrm{3}{d}=\mathrm{21} \\ $$$$\mathrm{3}\left(\mathrm{11}\right)−\mathrm{3}{d}=\mathrm{21}\Rightarrow{d}=\frac{\mathrm{33}−\mathrm{21}}{\mathrm{3}}=\mathrm{4} \\ $$$${first}\:{term}={a}={t}−\mathrm{2}{d}=\mathrm{11}−\mathrm{2}\left(\mathrm{4}\right)=\mathrm{3} \\ $$$${S}_{\mathrm{10}} =\frac{\mathrm{10}}{\mathrm{2}}\left[\mathrm{2}\left(\mathrm{3}\right)+\left(\mathrm{10}−\mathrm{1}\right)\left(\mathrm{4}\right)\right] \\ $$$$\:\:\:\:\:=\mathrm{5}\left(\mathrm{6}+\mathrm{36}\right)=\mathrm{210} \\ $$

Answered by Rasheed.Sindhi last updated on 06/Mar/23

Let u & t are 2nd & 3rd terms respectively. d is common difference. •(u−d)+u+(u+d)=21 3u=21⇒u=7 (2nd term) •(t−2d)+(t−d)+t+(t+d)+(t+2d)=55 5t=55⇒t=11 (3rd term) •d=t−u=11−7=4 • First term=u−d=7−4=3 • S_(10) =((10)/2)[2(3)+(10−1)(4)] =5(6+36)=5×42=210

$${Let}\:\:{u}\:\&\:{t}\:{are}\:\mathrm{2}{nd}\:\&\:\mathrm{3}{rd}\:{terms}\:{respectively}. \\ $$$${d}\:{is}\:{common}\:{difference}. \\ $$$$\bullet\left({u}−{d}\right)+{u}+\left({u}+{d}\right)=\mathrm{21} \\ $$$$\:\:\:\:\mathrm{3}{u}=\mathrm{21}\Rightarrow{u}=\mathrm{7}\:\:\left(\mathrm{2}{nd}\:{term}\right) \\ $$$$\bullet\left({t}−\mathrm{2}{d}\right)+\left({t}−{d}\right)+{t}+\left({t}+{d}\right)+\left({t}+\mathrm{2}{d}\right)=\mathrm{55} \\ $$$$\:\:\:\:\mathrm{5}{t}=\mathrm{55}\Rightarrow{t}=\mathrm{11}\:\:\left(\mathrm{3}{rd}\:{term}\right) \\ $$$$\bullet{d}={t}−{u}=\mathrm{11}−\mathrm{7}=\mathrm{4} \\ $$$$\bullet\:{First}\:{term}={u}−{d}=\mathrm{7}−\mathrm{4}=\mathrm{3} \\ $$$$\bullet\:{S}_{\mathrm{10}} =\frac{\mathrm{10}}{\mathrm{2}}\left[\mathrm{2}\left(\mathrm{3}\right)+\left(\mathrm{10}−\mathrm{1}\right)\left(\mathrm{4}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}\left(\mathrm{6}+\mathrm{36}\right)=\mathrm{5}×\mathrm{42}=\mathrm{210} \\ $$

Commented by Humble last updated on 07/Mar/23

thanks, sir.

$${thanks},\:{sir}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com