
Question Number 76872 by john santu last updated on 31/Dec/19
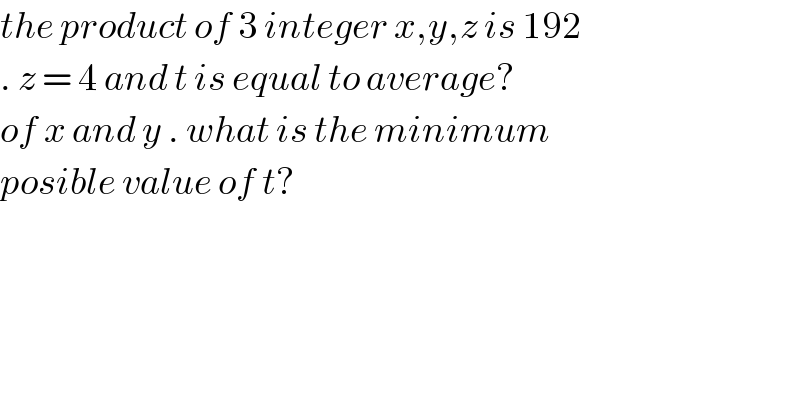
$${the}\:{product}\:{of}\:\mathrm{3}\:{integer}\:{x},{y},{z}\:{is}\:\mathrm{192} \\ $$$$.\:{z}\:=\:\mathrm{4}\:{and}\:{t}\:{is}\:{equal}\:{to}\:{average}? \\ $$$${of}\:{x}\:{and}\:{y}\:.\:{what}\:{is}\:{the}\:{minimum}\: \\ $$$${posible}\:{value}\:{of}\:{t}? \\ $$
Commented by mr W last updated on 31/Dec/19
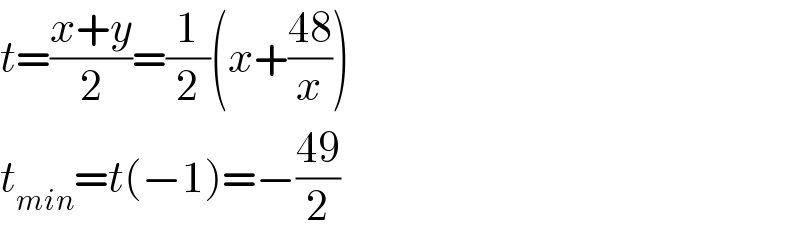
$${t}=\frac{{x}+{y}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\frac{\mathrm{48}}{{x}}\right) \\ $$$${t}_{{min}} ={t}\left(−\mathrm{1}\right)=−\frac{\mathrm{49}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 31/Dec/19
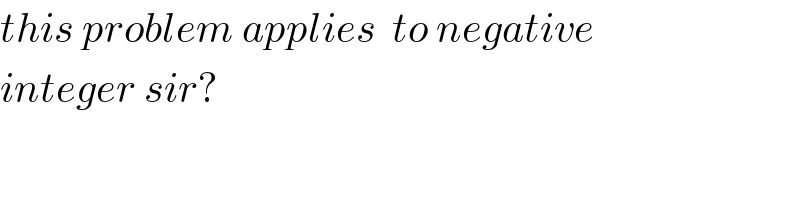
$${this}\:{problem}\:{applies}\:\:{to}\:{negative} \\ $$$${integer}\:{sir}? \\ $$
Commented by mr W last updated on 31/Dec/19
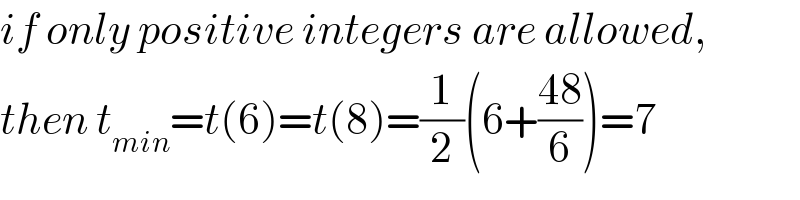
$${if}\:{only}\:{positive}\:{integers}\:{are}\:{allowed}, \\ $$$${then}\:{t}_{{min}} ={t}\left(\mathrm{6}\right)={t}\left(\mathrm{8}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{6}+\frac{\mathrm{48}}{\mathrm{6}}\right)=\mathrm{7} \\ $$
Commented by john santu last updated on 31/Dec/19

$${thanks}\:{sir} \\ $$
