Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 60426 by cesar.marval.larez@gmail.com last updated on 20/May/19

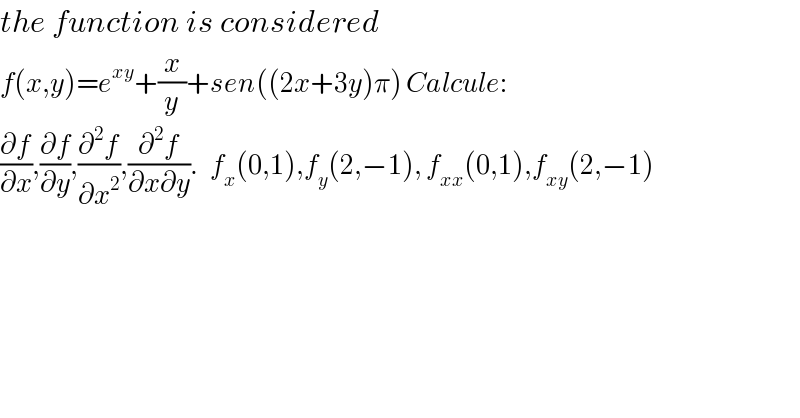
the function is considered f(x,y)=e^(xy) +(x/y)+sen((2x+3y)π) Calcule: (∂f/∂x),(∂f/∂y),(∂^2 f/∂x^2 ),(∂^2 f/(∂x∂y)). f_x (0,1),f_y (2,−1), f_(xx) (0,1),f_(xy) (2,−1)

$${the}\:{function}\:{is}\:{considered}\: \\ $$$${f}\left({x},{y}\right)={e}^{{xy}} +\frac{{x}}{{y}}+{sen}\left(\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\pi\right)\:{Calcule}: \\ $$$$\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}},\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} },\frac{\partial^{\mathrm{2}} {f}}{\partial{x}\partial{y}}.\:\:\:{f}_{{x}} \left(\mathrm{0},\mathrm{1}\right),{f}_{{y}} \left(\mathrm{2},−\mathrm{1}\right),\:{f}_{{xx}} \left(\mathrm{0},\mathrm{1}\right),{f}_{{xy}} \left(\mathrm{2},−\mathrm{1}\right) \\ $$

Commented by kaivan.ahmadi last updated on 21/May/19

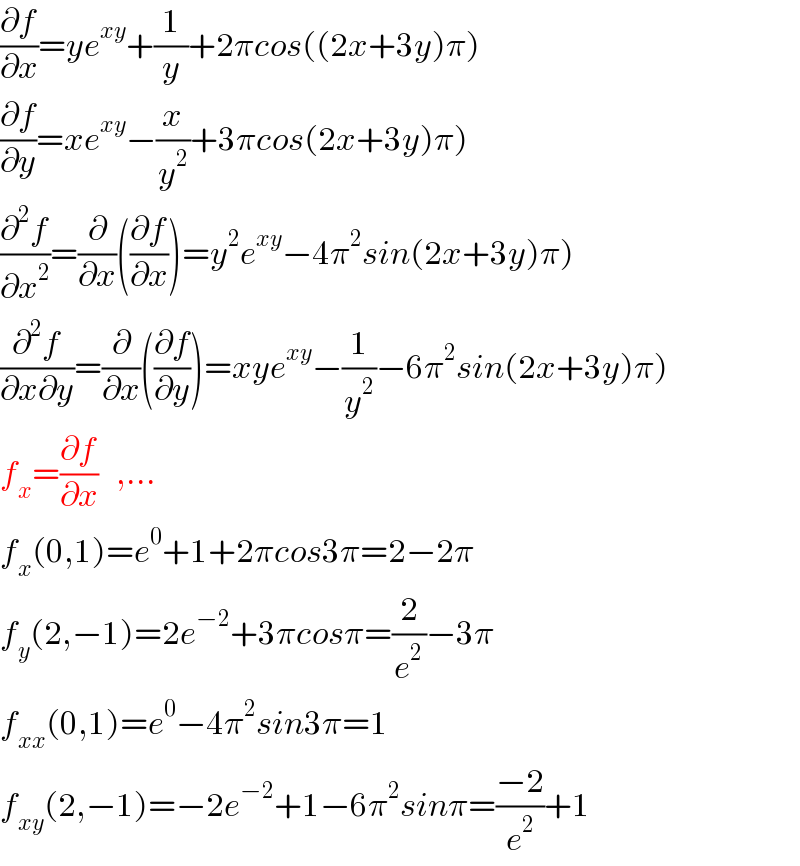
(∂f/∂x)=ye^(xy) +(1/y)+2πcos((2x+3y)π) (∂f/∂y)=xe^(xy) −(x/y^2 )+3πcos(2x+3y)π) (∂^2 f/∂x^2 )=(∂/∂x)((∂f/∂x))=y^2 e^(xy) −4π^2 sin(2x+3y)π) (∂^2 f/(∂x∂y))=(∂/∂x)((∂f/∂y))=xye^(xy) −(1/y^2 )−6π^2 sin(2x+3y)π) f_x =(∂f/∂x) ,... f_x (0,1)=e^0 +1+2πcos3π=2−2π f_y (2,−1)=2e^(−2) +3πcosπ=(2/e^2 )−3π f_(xx) (0,1)=e^0 −4π^2 sin3π=1 f_(xy) (2,−1)=−2e^(−2) +1−6π^2 sinπ=((−2)/e^2 )+1

$$\frac{\partial{f}}{\partial{x}}={ye}^{{xy}} +\frac{\mathrm{1}}{{y}}+\mathrm{2}\pi{cos}\left(\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\pi\right) \\ $$$$\left.\frac{\partial{f}}{\partial{y}}={xe}^{{xy}} −\frac{{x}}{{y}^{\mathrm{2}} }+\mathrm{3}\pi{cos}\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\pi\right) \\ $$$$\left.\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }=\frac{\partial}{\partial{x}}\left(\frac{\partial{f}}{\partial{x}}\right)={y}^{\mathrm{2}} {e}^{{xy}} −\mathrm{4}\pi^{\mathrm{2}} {sin}\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\pi\right) \\ $$$$\left.\frac{\partial^{\mathrm{2}} {f}}{\partial{x}\partial{y}}=\frac{\partial}{\partial{x}}\left(\frac{\partial{f}}{\partial{y}}\right)={xye}^{{xy}} −\frac{\mathrm{1}}{{y}^{\mathrm{2}} }−\mathrm{6}\pi^{\mathrm{2}} {sin}\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\pi\right) \\ $$$${f}_{{x}} =\frac{\partial{f}}{\partial{x}}\:\:\:,... \\ $$$${f}_{{x}} \left(\mathrm{0},\mathrm{1}\right)={e}^{\mathrm{0}} +\mathrm{1}+\mathrm{2}\pi{cos}\mathrm{3}\pi=\mathrm{2}−\mathrm{2}\pi \\ $$$${f}_{{y}} \left(\mathrm{2},−\mathrm{1}\right)=\mathrm{2}{e}^{−\mathrm{2}} +\mathrm{3}\pi{cos}\pi=\frac{\mathrm{2}}{{e}^{\mathrm{2}} }−\mathrm{3}\pi \\ $$$${f}_{{xx}} \left(\mathrm{0},\mathrm{1}\right)={e}^{\mathrm{0}} −\mathrm{4}\pi^{\mathrm{2}} {sin}\mathrm{3}\pi=\mathrm{1} \\ $$$${f}_{{xy}} \left(\mathrm{2},−\mathrm{1}\right)=−\mathrm{2}{e}^{−\mathrm{2}} +\mathrm{1}−\mathrm{6}\pi^{\mathrm{2}} {sin}\pi=\frac{−\mathrm{2}}{{e}^{\mathrm{2}} }+\mathrm{1} \\ $$

Commented by cesar.marval.larez@gmail.com last updated on 21/May/19

thanks sir for the solution

$${thanks}\:{sir}\:{for}\:{the}\:{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com