
Question Number 192991 by otchereabdullai@gmail.com last updated on 01/Jun/23

$${the}\:{first},\:{third}\:{and}\:{sixth}\:{terms}\:{of}\:{a} \\ $$$${linear}\:{sequence}\:{are}\:{the}\:{first}\:{three}\: \\ $$$${terms}\:{of}\:{an}\:{exponential}\:{sequence}.\: \\ $$$${find}\:{the}\:{common}\:{ratio} \\ $$
Answered by MM42 last updated on 01/Jun/23
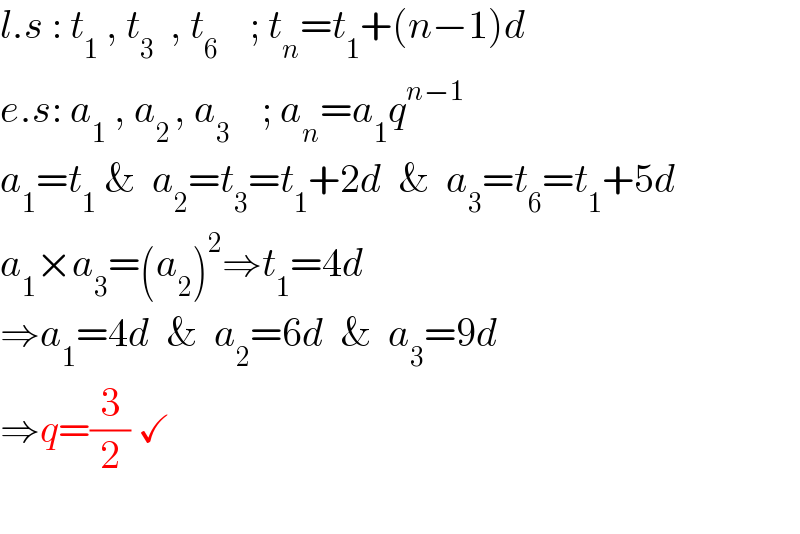
$${l}.{s}\::\:{t}_{\mathrm{1}} \:,\:{t}_{\mathrm{3}} \:\:,\:{t}_{\mathrm{6}} \:\:\:\:;\:{t}_{{n}} ={t}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d} \\ $$$${e}.{s}:\:{a}_{\mathrm{1}} \:,\:{a}_{\mathrm{2}\:} ,\:{a}_{\mathrm{3}} \:\:\:\:;\:{a}_{{n}} ={a}_{\mathrm{1}} {q}^{{n}−\mathrm{1}} \\ $$$${a}_{\mathrm{1}} ={t}_{\mathrm{1}} \:\&\:\:{a}_{\mathrm{2}} ={t}_{\mathrm{3}} ={t}_{\mathrm{1}} +\mathrm{2}{d}\:\:\&\:\:{a}_{\mathrm{3}} ={t}_{\mathrm{6}} ={t}_{\mathrm{1}} +\mathrm{5}{d} \\ $$$${a}_{\mathrm{1}} ×{a}_{\mathrm{3}} =\left({a}_{\mathrm{2}} \right)^{\mathrm{2}} \Rightarrow{t}_{\mathrm{1}} =\mathrm{4}{d} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\mathrm{4}{d}\:\:\&\:\:{a}_{\mathrm{2}} =\mathrm{6}{d}\:\:\&\:\:{a}_{\mathrm{3}} =\mathrm{9}{d} \\ $$$$\Rightarrow{q}=\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$$$ \\ $$
Commented by otchereabdullai@gmail.com last updated on 01/Jun/23

$${thanks} \\ $$
