Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 154240 by amin96 last updated on 15/Sep/21

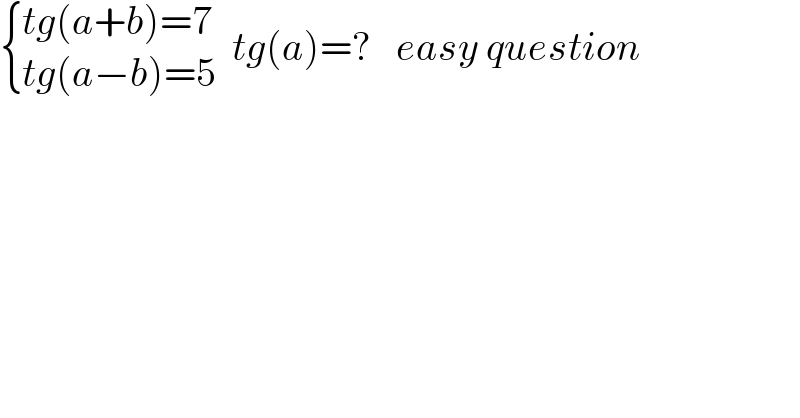
{ ((tg(a+b)=7)),((tg(a−b)=5)) :} tg(a)=? easy question

$$\begin{cases}{{tg}\left({a}+{b}\right)=\mathrm{7}}\\{{tg}\left({a}−{b}\right)=\mathrm{5}}\end{cases}\:\:{tg}\left({a}\right)=?\:\:\:{easy}\:{question} \\ $$

Answered by mr W last updated on 15/Sep/21

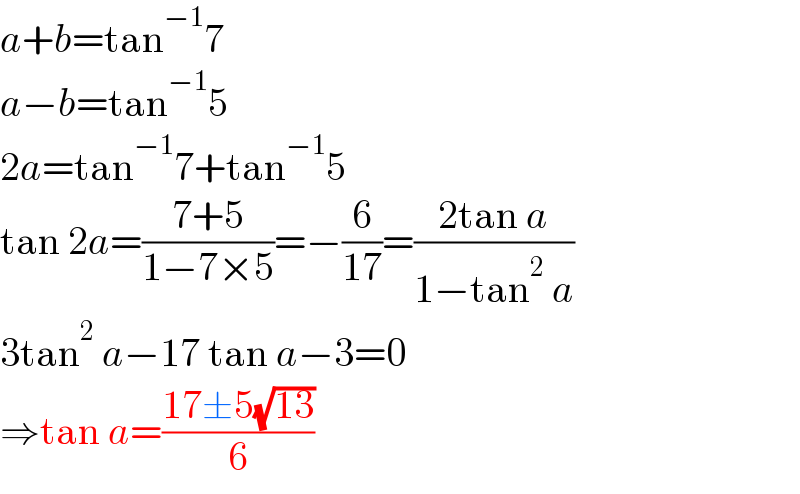
a+b=tan^(−1) 7 a−b=tan^(−1) 5 2a=tan^(−1) 7+tan^(−1) 5 tan 2a=((7+5)/(1−7×5))=−(6/(17))=((2tan a)/(1−tan^2 a)) 3tan^2 a−17 tan a−3=0 ⇒tan a=((17±5(√(13)))/6)

$${a}+{b}=\mathrm{tan}^{−\mathrm{1}} \mathrm{7} \\ $$$${a}−{b}=\mathrm{tan}^{−\mathrm{1}} \mathrm{5} \\ $$$$\mathrm{2}{a}=\mathrm{tan}^{−\mathrm{1}} \mathrm{7}+\mathrm{tan}^{−\mathrm{1}} \mathrm{5} \\ $$$$\mathrm{tan}\:\mathrm{2}{a}=\frac{\mathrm{7}+\mathrm{5}}{\mathrm{1}−\mathrm{7}×\mathrm{5}}=−\frac{\mathrm{6}}{\mathrm{17}}=\frac{\mathrm{2tan}\:{a}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{a}} \\ $$$$\mathrm{3tan}^{\mathrm{2}} \:{a}−\mathrm{17}\:\mathrm{tan}\:{a}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:{a}=\frac{\mathrm{17}\pm\mathrm{5}\sqrt{\mathrm{13}}}{\mathrm{6}} \\ $$

Commented by SLVR last updated on 26/Sep/21

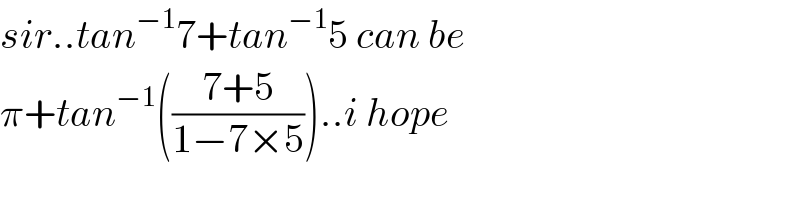
sir..tan^(−1) 7+tan^(−1) 5 can be π+tan^(−1) (((7+5)/(1−7×5)))..i hope

$${sir}..{tan}^{−\mathrm{1}} \mathrm{7}+{tan}^{−\mathrm{1}} \mathrm{5}\:{can}\:{be} \\ $$$$\pi+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}+\mathrm{5}}{\mathrm{1}−\mathrm{7}×\mathrm{5}}\right)..{i}\:{hope} \\ $$

Commented by SLVR last updated on 26/Sep/21

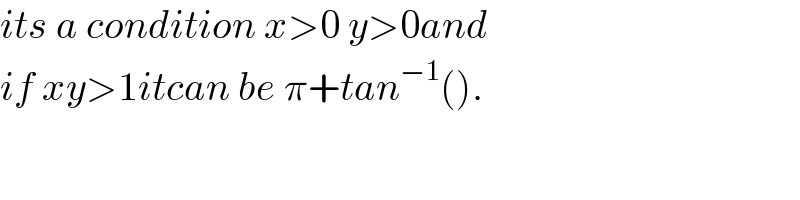
its a condition x>0 y>0and if xy>1itcan be π+tan^(−1) ().

$${its}\:{a}\:{condition}\:{x}>\mathrm{0}\:{y}>\mathrm{0}{and}\: \\ $$$${if}\:{xy}>\mathrm{1}{itcan}\:{be}\:\pi+{tan}^{−\mathrm{1}} \left(\right). \\ $$

Commented by mr W last updated on 26/Sep/21

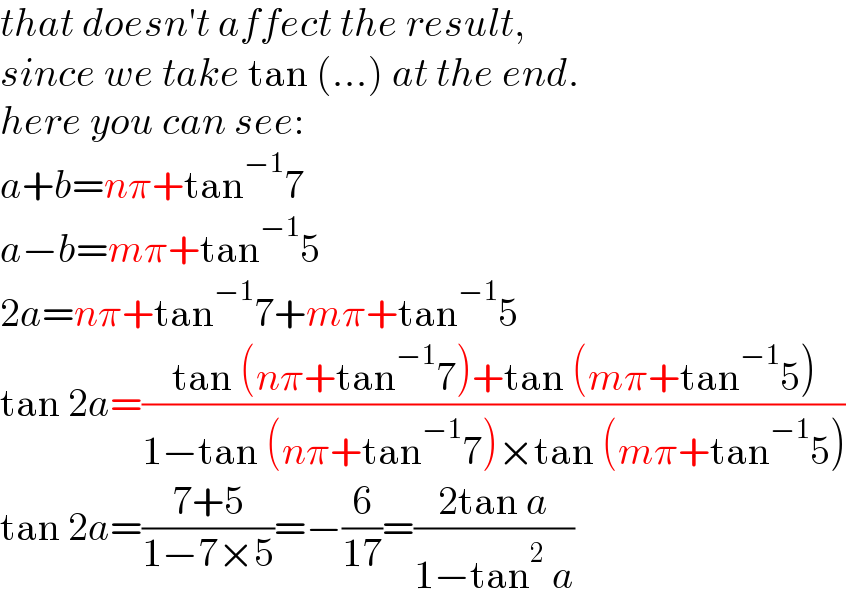
that doesn′t affect the result, since we take tan (...) at the end. here you can see: a+b=nπ+tan^(−1) 7 a−b=mπ+tan^(−1) 5 2a=nπ+tan^(−1) 7+mπ+tan^(−1) 5 tan 2a=((tan (nπ+tan^(−1) 7)+tan (mπ+tan^(−1) 5))/(1−tan (nπ+tan^(−1) 7)×tan (mπ+tan^(−1) 5))) tan 2a=((7+5)/(1−7×5))=−(6/(17))=((2tan a)/(1−tan^2 a))

$${that}\:{doesn}'{t}\:{affect}\:{the}\:{result}, \\ $$$${since}\:{we}\:{take}\:\mathrm{tan}\:\left(...\right)\:{at}\:{the}\:{end}. \\ $$$${here}\:{you}\:{can}\:{see}: \\ $$$${a}+{b}={n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{7} \\ $$$${a}−{b}={m}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{5} \\ $$$$\mathrm{2}{a}={n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{7}+{m}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{5} \\ $$$$\mathrm{tan}\:\mathrm{2}{a}=\frac{\mathrm{tan}\:\left({n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{7}\right)+\mathrm{tan}\:\left({m}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{5}\right)}{\mathrm{1}−\mathrm{tan}\:\left({n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{7}\right)×\mathrm{tan}\:\left({m}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{5}\right)} \\ $$$$\mathrm{tan}\:\mathrm{2}{a}=\frac{\mathrm{7}+\mathrm{5}}{\mathrm{1}−\mathrm{7}×\mathrm{5}}=−\frac{\mathrm{6}}{\mathrm{17}}=\frac{\mathrm{2tan}\:{a}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{a}} \\ $$

Commented by SLVR last updated on 26/Sep/21

wow...thats right...prof...W

$${wow}...{thats}\:{right}...{prof}...{W} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com