Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 76298 by benjo last updated on 26/Dec/19

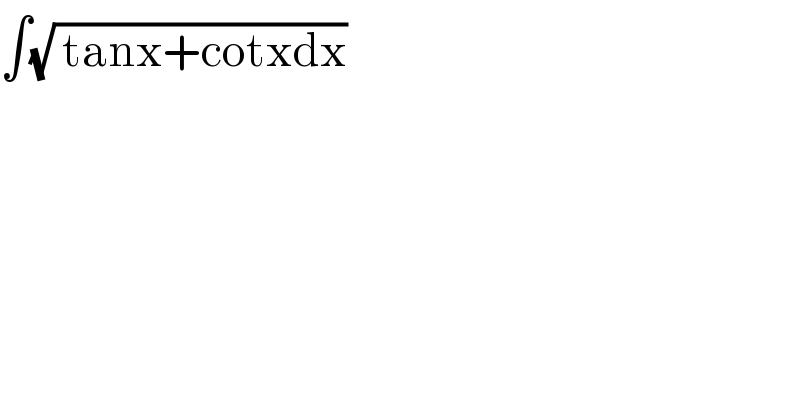
∫(√( tanx+cotxdx))

$$\int\sqrt{\:\mathrm{tanx}+\mathrm{cotxdx}} \\ $$

Commented by benjo last updated on 26/Dec/19

Commented by john santuy last updated on 26/Dec/19

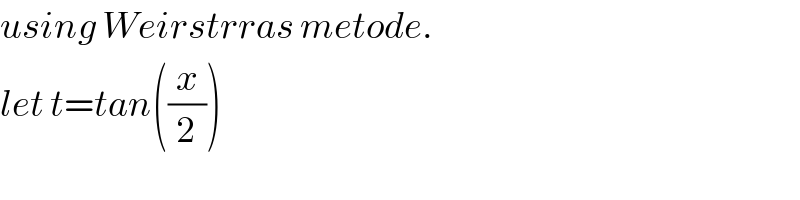
using Weirstrras metode. let t=tan((x/2))

$${using}\:{Weirstrras}\:{metode}. \\ $$$${let}\:{t}={tan}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$

Commented by benjo last updated on 26/Dec/19

please sir your write step by step

$$\mathrm{please}\:\mathrm{sir}\:\mathrm{your}\:\mathrm{write}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$

Commented by mathmax by abdo last updated on 26/Dec/19

let I =∫ (√(tanx+(1/(tanx))))dx ⇒ I =∫(√(((sinx)/(cosx))+((cosx)/(sinx))))dx =∫(√(1/(cosxsinx)))dx =∫(1/(√((1/2)sin(2x))))dx =∫ ((√2)/(√(sin(2x))))dx vhangement (√(sin(2x)))=t give I =∫((√2)/t)((tdt)/(√(1−t^4 ))) because sin(2x)=t^2 ⇒2x =arcsin(t^2 ) ⇒2dx=((2tdt)/(√(1−t^4 ))) ⇒ I =∫ (((√2)dt)/(√(1−t^4 ))) and this integral is not resoluble by elementary functions..

$${let}\:{I}\:=\int\:\sqrt{{tanx}+\frac{\mathrm{1}}{{tanx}}}{dx}\:\Rightarrow\:{I}\:=\int\sqrt{\frac{{sinx}}{{cosx}}+\frac{{cosx}}{{sinx}}}{dx} \\ $$$$=\int\sqrt{\frac{\mathrm{1}}{{cosxsinx}}}{dx}\:=\int\frac{\mathrm{1}}{\sqrt{\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)}}{dx}\:=\int\:\frac{\sqrt{\mathrm{2}}}{\sqrt{{sin}\left(\mathrm{2}{x}\right)}}{dx} \\ $$$${vhangement}\:\sqrt{{sin}\left(\mathrm{2}{x}\right)}={t}\:{give}\:{I}\:=\int\frac{\sqrt{\mathrm{2}}}{{t}}\frac{{tdt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:{because} \\ $$$${sin}\left(\mathrm{2}{x}\right)={t}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{x}\:={arcsin}\left({t}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{2}{dx}=\frac{\mathrm{2}{tdt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }} \\ $$$$\Rightarrow\:{I}\:=\int\:\frac{\sqrt{\mathrm{2}}{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:{and}\:{this}\:{integral}\:{is}\:{not}\:{resoluble}\:{by}\:{elementary} \\ $$$${functions}.. \\ $$

Answered by john santuy last updated on 26/Dec/19

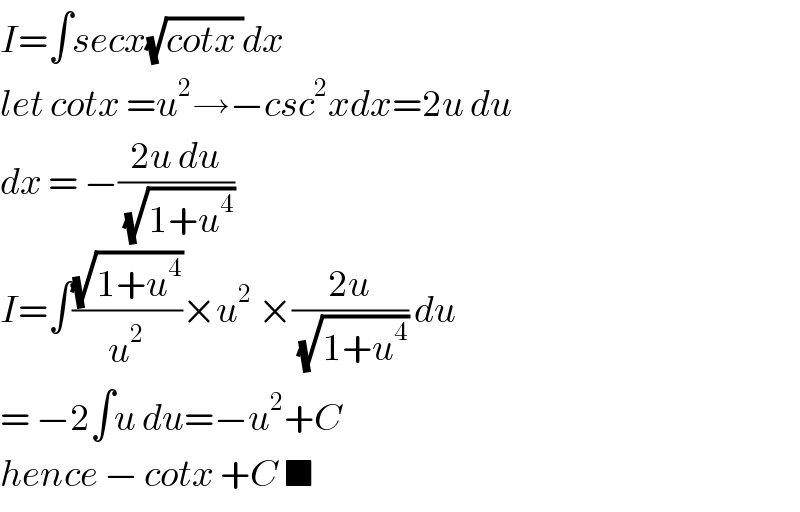
I=∫secx(√(cotx ))dx let cotx =u^2 →−csc^2 xdx=2u du dx = −((2u du)/(√(1+u^4 ))) I=∫((√(1+u^4 ))/u^2 )×u^2 ×((2u)/(√(1+u^4 ))) du = −2∫u du=−u^2 +C hence − cotx +C ■

$${I}=\int{secx}\sqrt{{cotx}\:}{dx} \\ $$$${let}\:{cotx}\:={u}^{\mathrm{2}} \rightarrow−{csc}^{\mathrm{2}} {xdx}=\mathrm{2}{u}\:{du} \\ $$$${dx}\:=\:−\frac{\mathrm{2}{u}\:{du}}{\sqrt{\mathrm{1}+{u}^{\mathrm{4}} }} \\ $$$${I}=\int\frac{\sqrt{\mathrm{1}+{u}^{\mathrm{4}} }}{{u}^{\mathrm{2}} }×{u}^{\mathrm{2}} \:×\frac{\mathrm{2}{u}}{\sqrt{\mathrm{1}+{u}^{\mathrm{4}} }}\:{du} \\ $$$$=\:−\mathrm{2}\int{u}\:{du}=−{u}^{\mathrm{2}} +{C} \\ $$$${hence}\:−\:{cotx}\:+{C}\:\blacksquare \\ $$

Commented by benjo last updated on 26/Dec/19

waw thanks sir

$$\mathrm{waw}\:\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 26/Dec/19

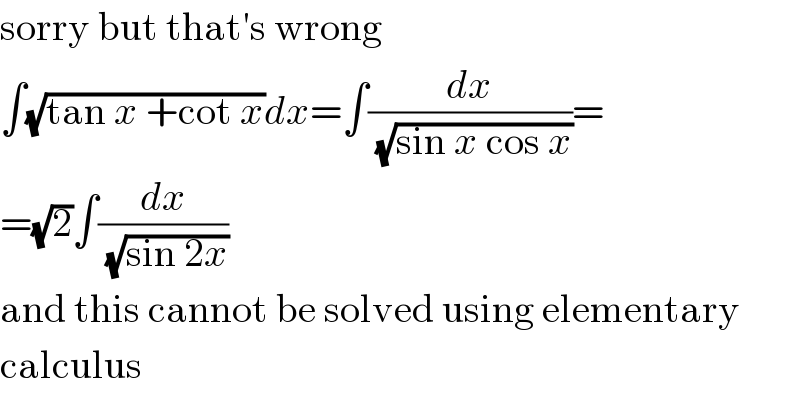
sorry but that′s wrong ∫(√(tan x +cot x))dx=∫(dx/(√(sin x cos x)))= =(√2)∫(dx/(√(sin 2x))) and this cannot be solved using elementary calculus

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{that}'\mathrm{s}\:\mathrm{wrong} \\ $$$$\int\sqrt{\mathrm{tan}\:{x}\:+\mathrm{cot}\:{x}}{dx}=\int\frac{{dx}}{\sqrt{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}}= \\ $$$$=\sqrt{\mathrm{2}}\int\frac{{dx}}{\sqrt{\mathrm{sin}\:\mathrm{2}{x}}} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{elementary} \\ $$$$\mathrm{calculus} \\ $$

Commented by MJS last updated on 26/Dec/19

but (d/dx)[−cot x]=csc^2 x ≠ sec x (√(cot x))

$$\mathrm{but}\:\frac{{d}}{{dx}}\left[−\mathrm{cot}\:{x}\right]=\mathrm{csc}^{\mathrm{2}} \:{x}\:\neq\:\mathrm{sec}\:{x}\:\sqrt{\mathrm{cot}\:{x}} \\ $$

Commented by john santu last updated on 26/Dec/19

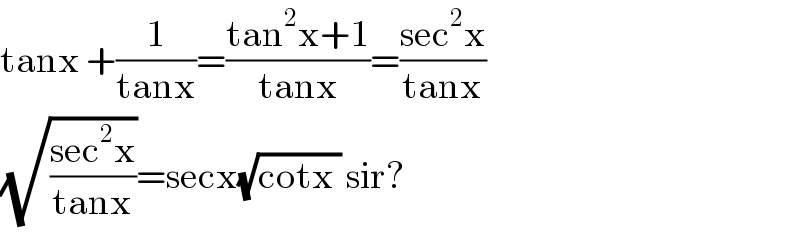
tanx +(1/(tanx))=((tan^2 x+1)/(tanx))=((sec^2 x)/(tanx)) (√((sec^2 x)/(tanx)))=secx(√(cotx )) sir?

$$\mathrm{tanx}\:+\frac{\mathrm{1}}{\mathrm{tanx}}=\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}{\mathrm{tanx}}=\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{tanx}} \\ $$$$\sqrt{\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{tanx}}}=\mathrm{secx}\sqrt{\mathrm{cotx}\:}\:\mathrm{sir}? \\ $$

Commented by john santu last updated on 26/Dec/19

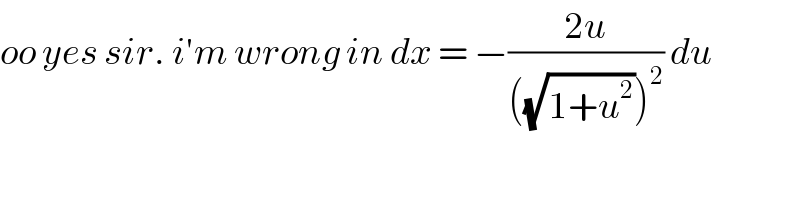
oo yes sir. i′m wrong in dx = −((2u)/(((√(1+u^2 )))^2 )) du

$${oo}\:{yes}\:{sir}.\:{i}'{m}\:{wrong}\:{in}\:{dx}\:=\:−\frac{\mathrm{2}{u}}{\left(\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{du} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com