
Question Number 112997 by malwan last updated on 10/Sep/20
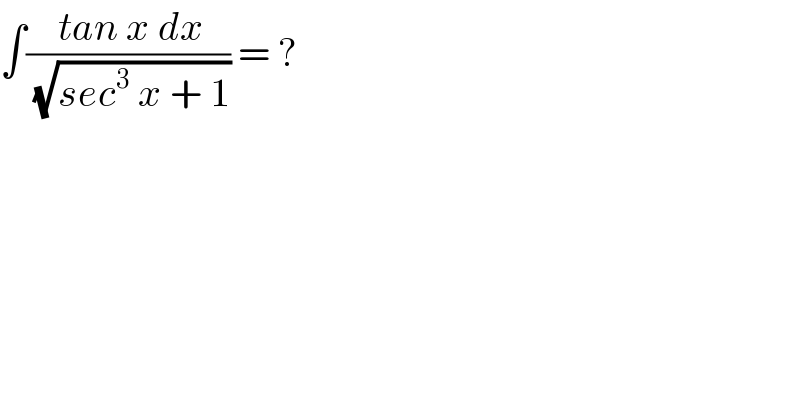
$$\int\frac{\:{tan}\:{x}\:{dx}}{\:\sqrt{{sec}^{\mathrm{3}} \:{x}\:+\:\mathrm{1}}}\:=\:? \\ $$
Commented by MJS_new last updated on 10/Sep/20
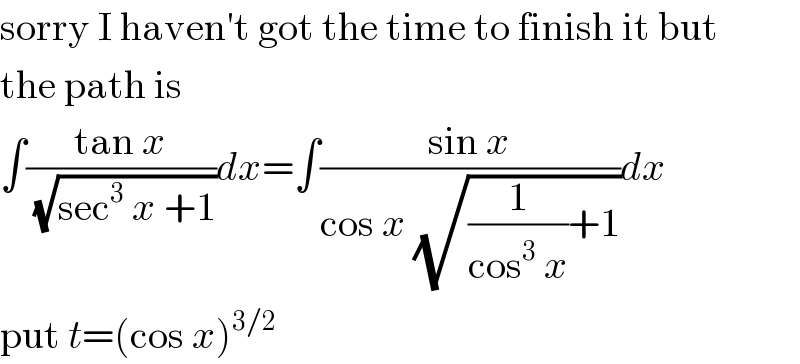
$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{got}\:\mathrm{the}\:\mathrm{time}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{it}\:\mathrm{but} \\ $$$$\mathrm{the}\:\mathrm{path}\:\mathrm{is} \\ $$$$\int\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{sec}^{\mathrm{3}} \:{x}\:+\mathrm{1}}}{dx}=\int\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}\:\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \:{x}}+\mathrm{1}}}{dx} \\ $$$$\mathrm{put}\:{t}=\left(\mathrm{cos}\:{x}\right)^{\mathrm{3}/\mathrm{2}} \\ $$
Commented by MJS_new last updated on 10/Sep/20
![∫((tan x)/( (√(sec^3 x +1))))= [t=(cos x)^(3/2) → dx=−((2dt)/(3sin x (√(cos x))))] =−(2/3)∫(dt/( (√(t^2 +1))))= [u=t+(√(t^2 +1)) → dt=((√(t^2 +1))/(t+(√(t^2 +1))))du] =−(2/3)∫(du/u)=−(2/3)ln u =−(2/3)ln (t+(√(t^2 +1))) = =−(2/3)ln ((cos x)^(3/2) +(√(1+cos^3 x))) +C](Q113033.png)
$$\int\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{sec}^{\mathrm{3}} \:{x}\:+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\left(\mathrm{cos}\:{x}\right)^{\mathrm{3}/\mathrm{2}} \:\rightarrow\:{dx}=−\frac{\mathrm{2}{dt}}{\mathrm{3sin}\:{x}\:\sqrt{\mathrm{cos}\:{x}}}\right] \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{du}\right] \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{du}}{{u}}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:{u}\:=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)\:= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\left(\left(\mathrm{cos}\:{x}\right)^{\mathrm{3}/\mathrm{2}} +\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{3}} \:{x}}\right)\:+{C} \\ $$
Commented by malwan last updated on 11/Sep/20
$${great}\:{Sir}\:{MJS} \\ $$$${thank}\:{you}\:{so}\:{much} \\ $$
Answered by malwan last updated on 11/Sep/20
![another way ∫(( tan x)/( (√(sec^3 x + 1))))dx=∫(( secx tanx)/(secx(√(sec^3 x+1))))dx = ∫(( du)/(u(√(u^3 +1)))) [u= sec x] v^2 =u^3 +1⇒2vdv=3u^2 du⇒du=((2vdv)/(3u^2 )) ∴∫(( 2vdv)/(3u^2 uv)) = (2/3)∫(( dv)/u^3 )=(2/3)∫(( dv)/(v^2 −1)) =(2/3) (1/2)ln∣((v−1)/(v+1))∣ + c = (1/3)ln∣(((√(u^3 +1)) −1)/( (√(u^3 +1)) +1))∣ + c =(1/3)ln∣(((√(sec^3 x+1)) −1)/( (√(sec^3 x+1)) +1))∣ +c](Q113102.png)
$${another}\:{way} \\ $$$$\int\frac{\:{tan}\:{x}}{\:\sqrt{{sec}^{\mathrm{3}} {x}\:+\:\mathrm{1}}}{dx}=\int\frac{\:{secx}\:{tanx}}{{secx}\sqrt{{sec}^{\mathrm{3}} {x}+\mathrm{1}}}{dx} \\ $$$$=\:\int\frac{\:{du}}{{u}\sqrt{{u}^{\mathrm{3}} +\mathrm{1}}}\:\left[{u}=\:{sec}\:{x}\right] \\ $$$${v}^{\mathrm{2}} ={u}^{\mathrm{3}} +\mathrm{1}\Rightarrow\mathrm{2}{vdv}=\mathrm{3}{u}^{\mathrm{2}} {du}\Rightarrow{du}=\frac{\mathrm{2}{vdv}}{\mathrm{3}{u}^{\mathrm{2}} } \\ $$$$\therefore\int\frac{\:\mathrm{2}{vdv}}{\mathrm{3}{u}^{\mathrm{2}} {uv}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\:{dv}}{{u}^{\mathrm{3}} }=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\:{dv}}{{v}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{v}−\mathrm{1}}{{v}+\mathrm{1}}\mid\:+\:{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\frac{\sqrt{{u}^{\mathrm{3}} +\mathrm{1}}\:−\mathrm{1}}{\:\sqrt{{u}^{\mathrm{3}} +\mathrm{1}}\:+\mathrm{1}}\mid\:+\:{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\frac{\sqrt{{sec}^{\mathrm{3}} {x}+\mathrm{1}}\:−\mathrm{1}}{\:\sqrt{{sec}^{\mathrm{3}} {x}+\mathrm{1}}\:+\mathrm{1}}\mid\:+{c} \\ $$
