
Question Number 197944 by liuxinnan last updated on 05/Oct/23
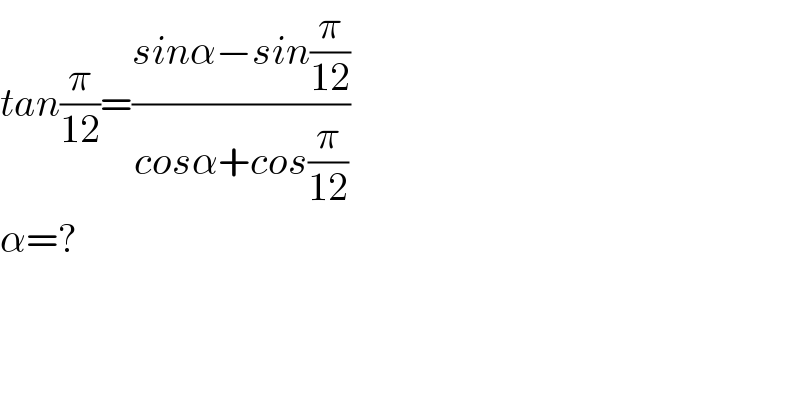
$${tan}\frac{\pi}{\mathrm{12}}=\frac{{sin}\alpha−{sin}\frac{\pi}{\mathrm{12}}}{{cos}\alpha+{cos}\frac{\pi}{\mathrm{12}}} \\ $$$$\alpha=? \\ $$
Answered by MM42 last updated on 05/Oct/23
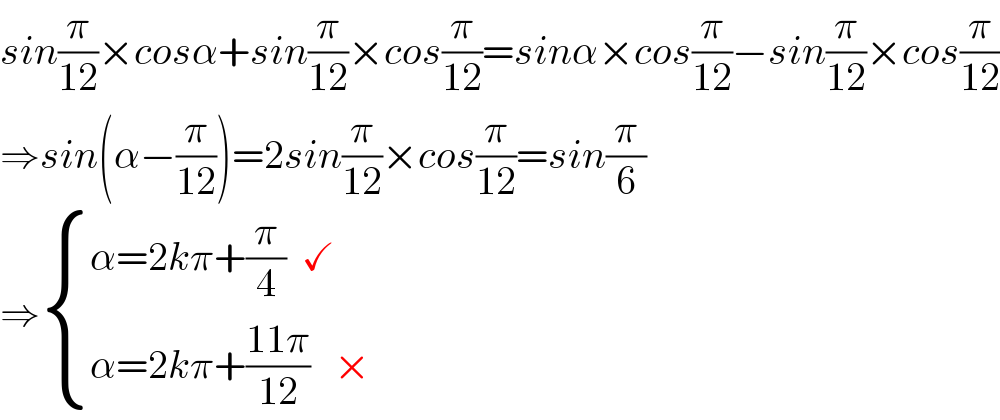
$${sin}\frac{\pi}{\mathrm{12}}×{cos}\alpha+{sin}\frac{\pi}{\mathrm{12}}×{cos}\frac{\pi}{\mathrm{12}}={sin}\alpha×{cos}\frac{\pi}{\mathrm{12}}−{sin}\frac{\pi}{\mathrm{12}}×{cos}\frac{\pi}{\mathrm{12}} \\ $$$$\Rightarrow{sin}\left(\alpha−\frac{\pi}{\mathrm{12}}\right)=\mathrm{2}{sin}\frac{\pi}{\mathrm{12}}×{cos}\frac{\pi}{\mathrm{12}}={sin}\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow\begin{cases}{\alpha=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}\:\:\checkmark}\\{\alpha=\mathrm{2}{k}\pi+\frac{\mathrm{11}\pi}{\mathrm{12}}\:\:\:×}\end{cases}\:\:\: \\ $$
Commented by MM42 last updated on 05/Oct/23
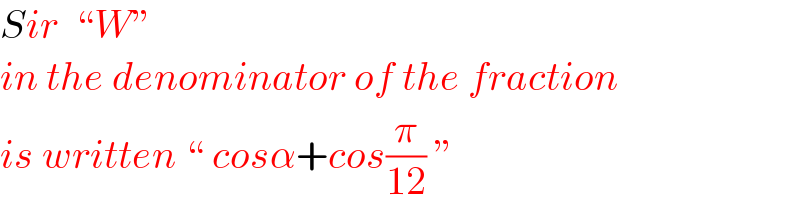
$${Sir}\:\:``{W}'' \\ $$$${in}\:{the}\:{denominator}\:{of}\:{the}\:{fraction} \\ $$$${is}\:{written}\:``\:{cos}\alpha+{cos}\frac{\pi}{\mathrm{12}}\:'' \\ $$
Commented by mr W last updated on 06/Oct/23
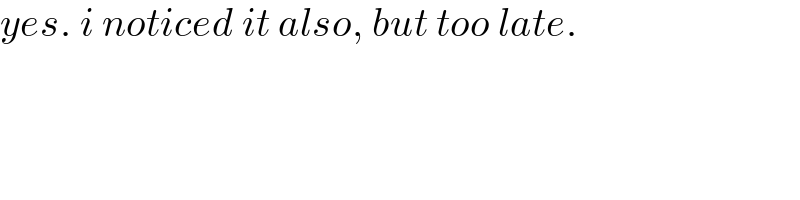
$${yes}.\:{i}\:{noticed}\:{it}\:{also},\:{but}\:{too}\:{late}. \\ $$
Commented by MM42 last updated on 06/Oct/23

$$\:\cancel{\lesseqgtr\underbrace{\boldsymbol{\mathrm{M}}}} \\ $$
