
Question Number 100189 by Dwaipayan Shikari last updated on 25/Jun/20

$$\int{tan}^{{i}} {xdx} \\ $$
Answered by maths mind last updated on 25/Jun/20
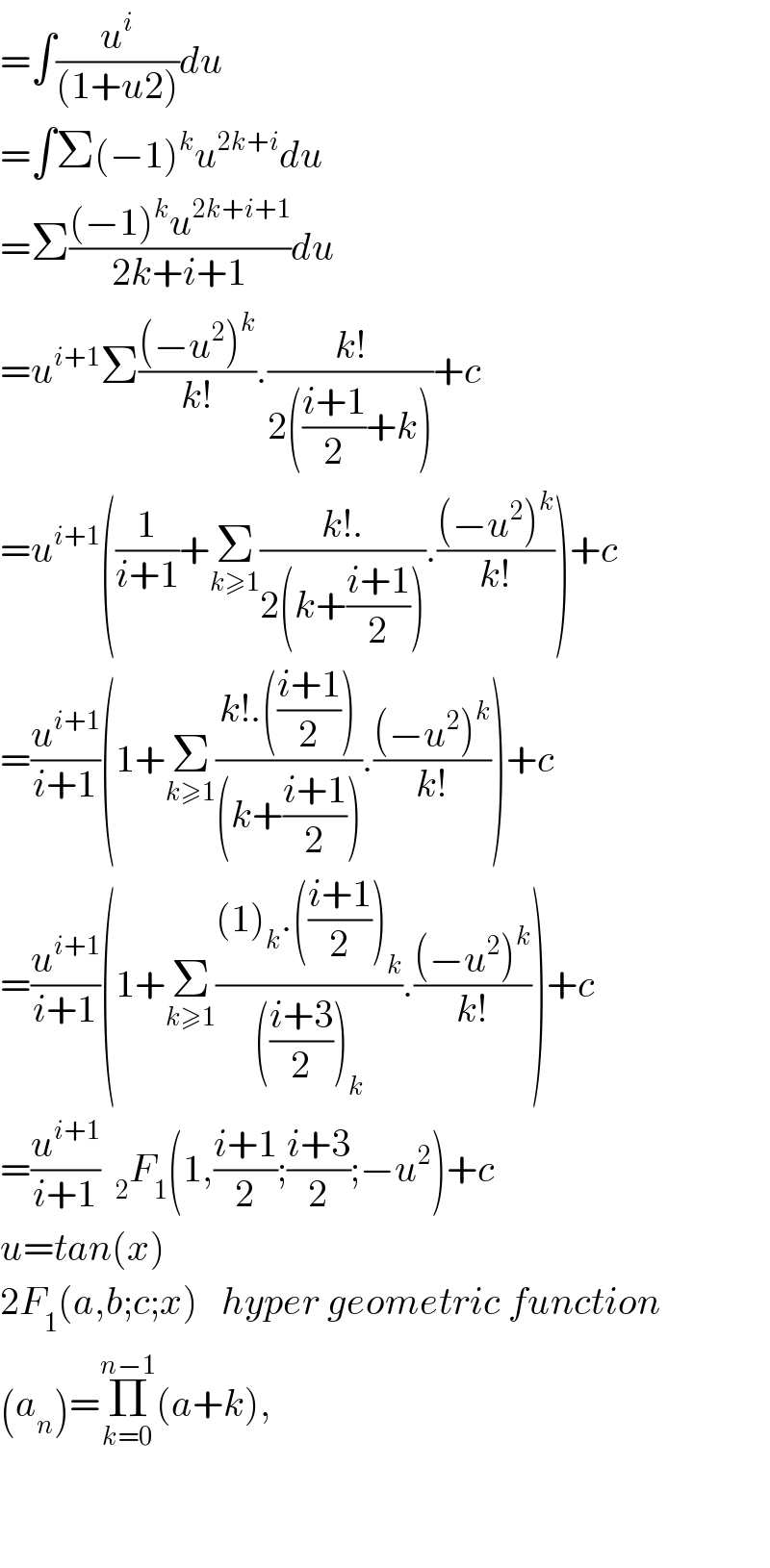
$$=\int\frac{{u}^{{i}} }{\left(\mathrm{1}+{u}\mathrm{2}\right)}{du} \\ $$$$=\int\Sigma\left(−\mathrm{1}\right)^{{k}} {u}^{\mathrm{2}{k}+{i}} {du} \\ $$$$=\Sigma\frac{\left(−\mathrm{1}\right)^{{k}} {u}^{\mathrm{2}{k}+{i}+\mathrm{1}} }{\mathrm{2}{k}+{i}+\mathrm{1}}{du} \\ $$$$={u}^{{i}+\mathrm{1}} \Sigma\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{{k}!}.\frac{{k}!}{\mathrm{2}\left(\frac{{i}+\mathrm{1}}{\mathrm{2}}+{k}\right)}+{c} \\ $$$$={u}^{{i}+\mathrm{1}} \left(\frac{\mathrm{1}}{{i}+\mathrm{1}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{k}!.}{\mathrm{2}\left({k}+\frac{{i}+\mathrm{1}}{\mathrm{2}}\right)}.\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{{k}!}\right)+{c} \\ $$$$=\frac{{u}^{{i}+\mathrm{1}} }{{i}+\mathrm{1}}\left(\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{k}!.\left(\frac{{i}+\mathrm{1}}{\mathrm{2}}\right)}{\left({k}+\frac{{i}+\mathrm{1}}{\mathrm{2}}\right)}.\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{{k}!}\right)+{c} \\ $$$$=\frac{{u}^{{i}+\mathrm{1}} }{{i}+\mathrm{1}}\left(\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{1}\right)_{{k}} .\left(\frac{{i}+\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{\left(\frac{{i}+\mathrm{3}}{\mathrm{2}}\right)_{{k}} }.\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{{k}!}\right)+{c} \\ $$$$=\frac{{u}^{{i}+\mathrm{1}} }{{i}+\mathrm{1}}\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{1},\frac{{i}+\mathrm{1}}{\mathrm{2}};\frac{{i}+\mathrm{3}}{\mathrm{2}};−{u}^{\mathrm{2}} \right)+{c} \\ $$$${u}={tan}\left({x}\right) \\ $$$$\mathrm{2}{F}_{\mathrm{1}} \left({a},{b};{c};{x}\right)\:\:\:{hyper}\:{geometric}\:{function} \\ $$$$\left({a}_{{n}} \right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({a}+{k}\right), \\ $$$$ \\ $$$$ \\ $$
