
Question Number 45669 by arvinddayama01@gmail.com last updated on 15/Oct/18
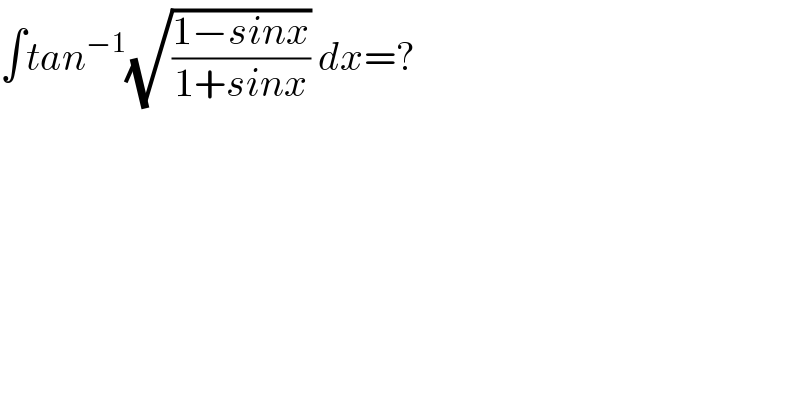
$$\int{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{sinx}}{\mathrm{1}+{sinx}}}\:{dx}=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18
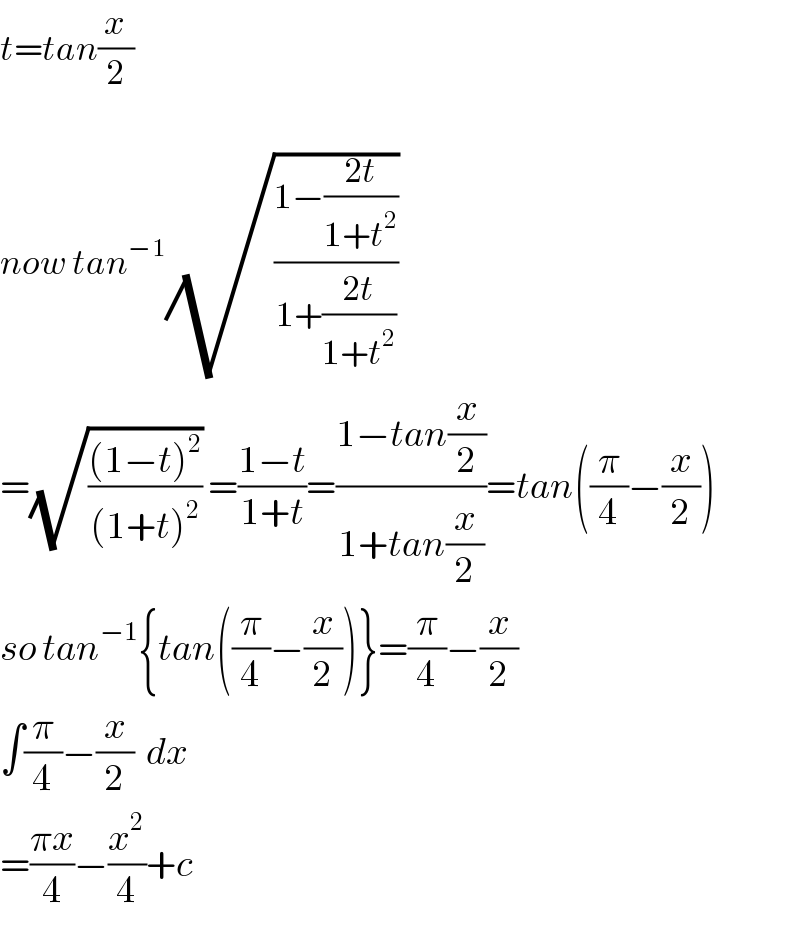
$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:\: \\ $$$$ \\ $$$${now}\:{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}}\: \\ $$$$=\sqrt{\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }}\:=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}=\frac{\mathrm{1}−{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}\frac{{x}}{\mathrm{2}}}={tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right) \\ $$$${so}\:{tan}^{−\mathrm{1}} \left\{{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\right\}=\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}} \\ $$$$\int\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\:\:{dx} \\ $$$$=\frac{\pi{x}}{\mathrm{4}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{c} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18

$${most}\:{welcome}... \\ $$
Commented by arvinddayama01@gmail.com last updated on 15/Oct/18
$${Thanku}\:{very}\:{much} \\ $$
Answered by vermasir last updated on 16/Oct/18
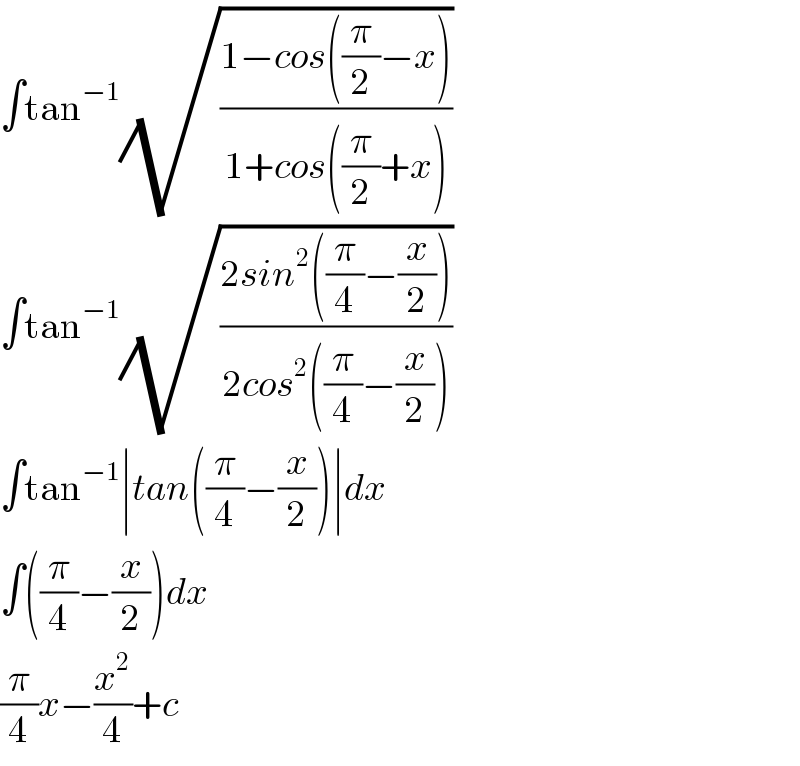
$$\int\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{2}}+{x}\right)}} \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}} \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \mid{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\mid{dx} \\ $$$$\int\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\frac{\pi}{\mathrm{4}}{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{c} \\ $$
