
Question Number 215527 by alephnull last updated on 09/Jan/25

$${t}_{\mathrm{33}} '{ab}+{t}_{\mathrm{00}} '{ab}=? \\ $$$$ \\ $$$$\mathrm{Clearing}\:\mathrm{up}\:\mathrm{defintions}: \\ $$$${t}_{\mathrm{33}} '{a}=\left({a}−\sqrt{\mathrm{36}}\right)×\mathrm{3} \\ $$$${t}_{\mathrm{00}} '{a}=\left({a}−\sqrt{\mathrm{36}}\right)×\mathrm{0} \\ $$$${t}'{a}={a}−\sqrt{\mathrm{36}} \\ $$$${t}'{a}=\:``\mathrm{transformation}''\:\mathrm{of}\:{a} \\ $$
Answered by MrGaster last updated on 10/Jan/25
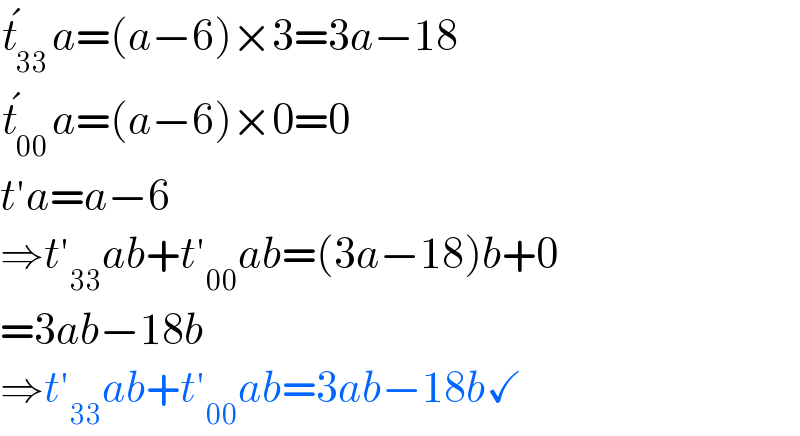
$$\acute {{t}}_{\mathrm{33}} {a}=\left({a}−\mathrm{6}\right)×\mathrm{3}=\mathrm{3}{a}−\mathrm{18} \\ $$$$\acute {{t}}_{\mathrm{00}} {a}=\left({a}−\mathrm{6}\right)×\mathrm{0}=\mathrm{0} \\ $$$${t}'{a}={a}−\mathrm{6} \\ $$$$\Rightarrow{t}'_{\mathrm{33}} {ab}+{t}'_{\mathrm{00}} {ab}=\left(\mathrm{3}{a}−\mathrm{18}\right){b}+\mathrm{0} \\ $$$$=\mathrm{3}{ab}−\mathrm{18}{b} \\ $$$$\Rightarrow{t}'_{\mathrm{33}} {ab}+{t}'_{\mathrm{00}} {ab}=\mathrm{3}{ab}−\mathrm{18}{b}\checkmark \\ $$
Commented by alephnull last updated on 10/Jan/25
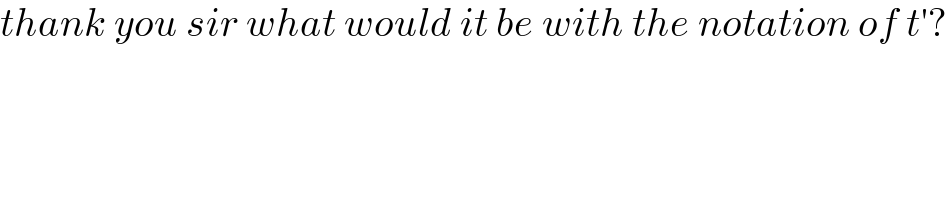
$${thank}\:{you}\:{sir}\:{what}\:{would}\:{it}\:{be}\:{with}\:{the}\:{notation}\:{of}\:{t}'? \\ $$
