
Previous in Relation and Functions Next in Relation and Functions
Question Number 62204 by maxmathsup by imad last updated on 17/Jun/19
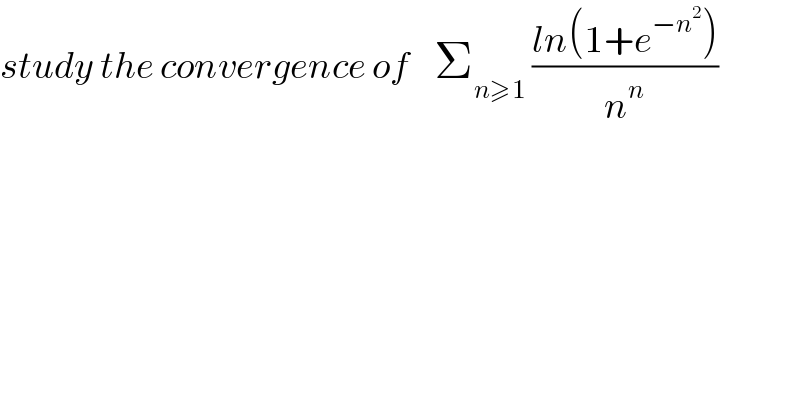
$${study}\:{the}\:{convergence}\:{of}\:\:\:\:\sum_{{n}\geqslant\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{e}^{−{n}^{\mathrm{2}} } \right)}{{n}^{{n}} } \\ $$
Commented by maxmathsup by imad last updated on 19/Jun/19
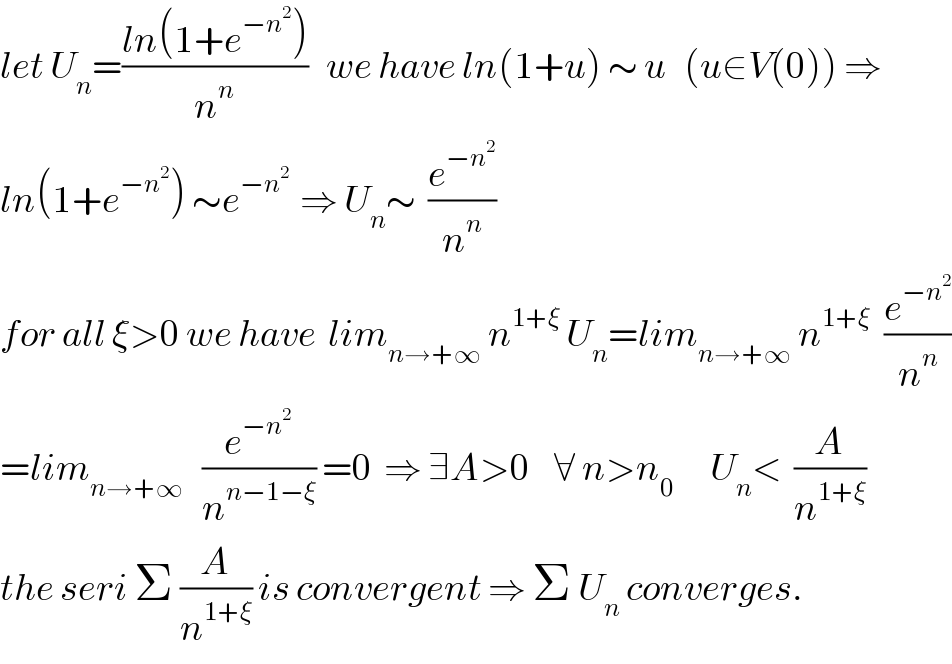
$${let}\:{U}_{{n}} =\frac{{ln}\left(\mathrm{1}+{e}^{−{n}^{\mathrm{2}} } \right)}{{n}^{{n}} }\:\:\:{we}\:{have}\:{ln}\left(\mathrm{1}+{u}\right)\:\sim\:{u}\:\:\:\left({u}\in{V}\left(\mathrm{0}\right)\right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{e}^{−{n}^{\mathrm{2}} } \right)\:\sim{e}^{−{n}^{\mathrm{2}} \:} \:\Rightarrow\:{U}_{{n}} \sim\:\:\frac{{e}^{−{n}^{\mathrm{2}} } }{{n}^{{n}} } \\ $$$${for}\:{all}\:\xi>\mathrm{0}\:{we}\:{have}\:\:{lim}_{{n}\rightarrow+\infty} \:{n}^{\mathrm{1}+\xi} \:{U}_{{n}} ={lim}_{{n}\rightarrow+\infty} \:{n}^{\mathrm{1}+\xi\:\:} \:\frac{{e}^{−{n}^{\mathrm{2}} } }{{n}^{{n}} } \\ $$$$={lim}_{{n}\rightarrow+\infty} \:\:\:\frac{{e}^{−{n}^{\mathrm{2}} } }{{n}^{{n}−\mathrm{1}−\xi} }\:=\mathrm{0}\:\:\Rightarrow\:\exists{A}>\mathrm{0}\:\:\:\:\forall\:{n}>{n}_{\mathrm{0}} \:\:\:\:\:\:{U}_{{n}} <\:\:\frac{{A}}{{n}^{\mathrm{1}+\xi} } \\ $$$${the}\:{seri}\:\Sigma\:\frac{{A}}{{n}^{\mathrm{1}+\xi} }\:{is}\:{convergent}\:\Rightarrow\:\Sigma\:{U}_{{n}} \:{converges}. \\ $$
