Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 199707 by SANOGO last updated on 08/Nov/23

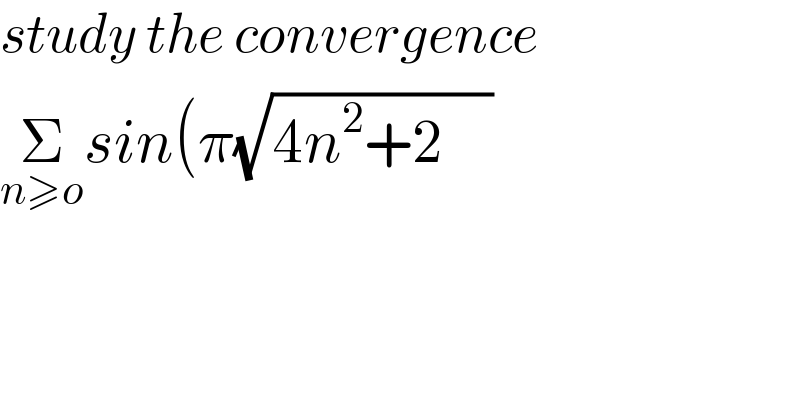
study the convergence Σ_(n≥o) ^ sin(π(√(4n^2 +2 ))

$${study}\:{the}\:{convergence} \\ $$$$\underset{{n}\geqslant{o}} {\overset{} {\sum}}{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{2}\:\:\:\:}\right. \\ $$

Answered by witcher3 last updated on 09/Nov/23

(√(4n^2 +2))=2n(√(1+(1/(2n^2 )))) sin(2πn(√(1+(1/(2n^2 )))))=sin(2πn(√(1+(1/(2n^2 ))))−2πn) =sin(2πn((√(1+(1/(2n^2 ))))−1) (√(1+(1/(2n^2 ))))−1=(1/(2n^2 ((√(1+(1/(2n^2 ))))+1)))≤(1/(4n^2 )) sin(0)≤sin(2πn(√(1+(1/(2n^2 ))))−2πn)≤sin((π/(2n^2 )))≤sin((π/2)) positiv serie 2πn((√(1+(1/(2n^2 )))))−2πn =2πn(1+(1/(2n^2 ))−1+o((1/n^2 ))=(π/n)+o((1/n)) sin((π/n)+o((1/n)))∼(π/n);Σ(π/n) dv⇒Σsin(π(√(4n^2 +2))) dv

$$\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{2}}=\mathrm{2n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }} \\ $$$$\mathrm{sin}\left(\mathrm{2}\pi\mathrm{n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}\right)=\mathrm{sin}\left(\mathrm{2}\pi\mathrm{n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}−\mathrm{2}\pi\mathrm{n}\right) \\ $$$$=\mathrm{sin}\left(\mathrm{2}\pi\mathrm{n}\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}−\mathrm{1}\right)\right. \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} \left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}+\mathrm{1}\right)}\leqslant\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} } \\ $$$$\mathrm{sin}\left(\mathrm{0}\right)\leqslant\mathrm{sin}\left(\mathrm{2}\pi\mathrm{n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}−\mathrm{2}\pi\mathrm{n}\right)\leqslant\mathrm{sin}\left(\frac{\pi}{\mathrm{2n}^{\mathrm{2}} }\right)\leqslant\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{positiv}\:\mathrm{serie} \\ $$$$\mathrm{2}\pi\mathrm{n}\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }}\right)−\mathrm{2}\pi\mathrm{n} \\ $$$$=\mathrm{2}\pi\mathrm{n}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }−\mathrm{1}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right. \\ $$$$\mathrm{sin}\left(\frac{\pi}{\mathrm{n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right)\sim\frac{\pi}{\mathrm{n}};\Sigma\frac{\pi}{\mathrm{n}}\:\:\mathrm{dv}\Rightarrow\Sigma\mathrm{sin}\left(\pi\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{2}}\right)\:\mathrm{dv} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com