Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214566 by mr W last updated on 12/Dec/24

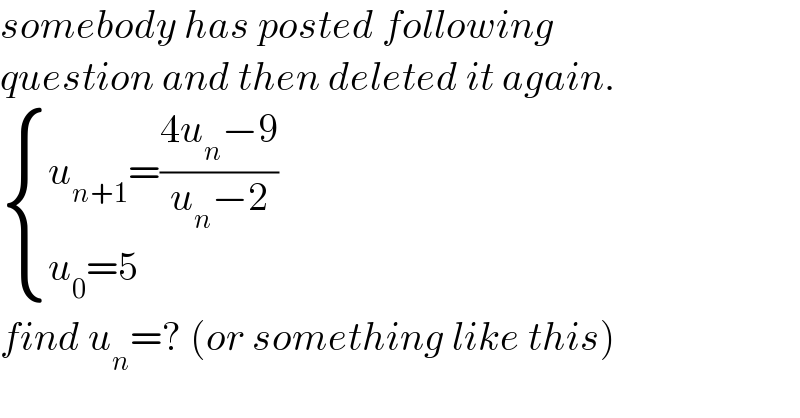
somebody has posted following question and then deleted it again. { ((u_(n+1) =((4u_n −9)/(u_n −2)))),((u_0 =5)) :} find u_n =? (or something like this)

$${somebody}\:{has}\:{posted}\:{following} \\ $$$${question}\:{and}\:{then}\:{deleted}\:{it}\:{again}. \\ $$$$\begin{cases}{{u}_{{n}+\mathrm{1}} =\frac{\mathrm{4}{u}_{{n}} −\mathrm{9}}{{u}_{{n}} −\mathrm{2}}}\\{{u}_{\mathrm{0}} =\mathrm{5}}\end{cases} \\ $$$${find}\:{u}_{{n}} =?\:\left({or}\:{something}\:{like}\:{this}\right) \\ $$

Answered by Hanuda354 last updated on 12/Dec/24

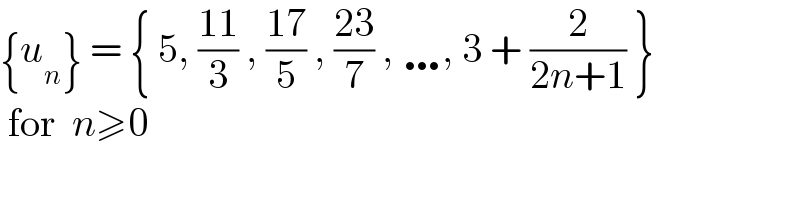
{u_n } = { 5, ((11)/3) , ((17)/5) , ((23)/7) , …, 3 + (2/(2n+1)) } for n≥0

$$\left\{{u}_{{n}} \right\}\:=\:\left\{\:\mathrm{5},\:\frac{\mathrm{11}}{\mathrm{3}}\:,\:\frac{\mathrm{17}}{\mathrm{5}}\:,\:\frac{\mathrm{23}}{\mathrm{7}}\:,\:\ldots,\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\right\} \\ $$$$\:\mathrm{for}\:\:{n}\geqslant\mathrm{0}\: \\ $$

Commented by mr W last updated on 12/Dec/24

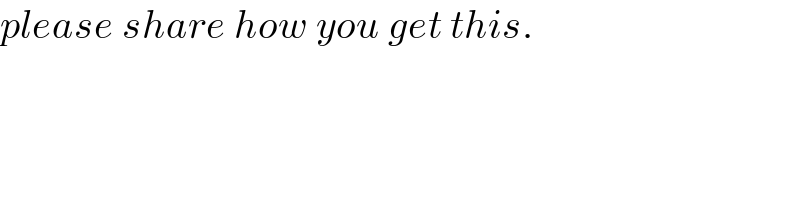
please share how you get this.

$${please}\:{share}\:{how}\:{you}\:{get}\:{this}. \\ $$

Commented by Hanuda354 last updated on 13/Dec/24

Using iteration, we get: u_1 = ((4(5)−9)/(5−2)) = ((11)/3) u_2 = ((4(((11)/3))−9)/(((11)/3)−2)) = ((17)/5) u_3 = ((4(((17)/5))−9)/(((17)/5)−2)) = ((23)/7) u_4 = ((4(((23)/7))−9)/(((23)/7)−2)) = ((29)/9) ⋮ u_n = ((6n+5)/(2n+1)) = 3 + (2/(2n+1)) By observing the pattern, we can conjecture a general formula u_n : u_n = 3 + (2/(2n+1)) Proof by Induction: Base case: u_0 = 3+(2/(2(0)+1)) = 5 Assume the formula holds for n=k , i.e, u_k = 3 + (2/(2k+1)) . We need to prove it holds for n = k+1. u_(k+1) = ((4u_k − 9)/(u_k − 2)) = ((4(3+(2/(2k+1)))−9)/(3+(2/(2k+1)) − 2)) Simplifying the expression, we get: u_(k+1) = ((3 + (8/(2k+1)))/(1 + (2/(2k+1)))) = ((6k+11)/(2k+3)) = 3 + (2/(2(k+1)+1)) This matches the formula for n = k+1 . Therefore, the solution to the recurrence relation is: u_n = 3 + (2/(2n+1))

$$\mathrm{Using}\:\:\mathrm{iteration},\:\mathrm{we}\:\mathrm{get}: \\ $$$${u}_{\mathrm{1}} \:=\:\frac{\mathrm{4}\left(\mathrm{5}\right)−\mathrm{9}}{\mathrm{5}−\mathrm{2}}\:=\:\frac{\mathrm{11}}{\mathrm{3}} \\ $$$${u}_{\mathrm{2}} \:=\:\frac{\mathrm{4}\left(\frac{\mathrm{11}}{\mathrm{3}}\right)−\mathrm{9}}{\frac{\mathrm{11}}{\mathrm{3}}−\mathrm{2}}\:=\:\frac{\mathrm{17}}{\mathrm{5}} \\ $$$${u}_{\mathrm{3}} \:=\:\frac{\mathrm{4}\left(\frac{\mathrm{17}}{\mathrm{5}}\right)−\mathrm{9}}{\frac{\mathrm{17}}{\mathrm{5}}−\mathrm{2}}\:=\:\frac{\mathrm{23}}{\mathrm{7}} \\ $$$${u}_{\mathrm{4}} \:=\:\frac{\mathrm{4}\left(\frac{\mathrm{23}}{\mathrm{7}}\right)−\mathrm{9}}{\frac{\mathrm{23}}{\mathrm{7}}−\mathrm{2}}\:=\:\frac{\mathrm{29}}{\mathrm{9}} \\ $$$$\vdots \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{6}{n}+\mathrm{5}}{\mathrm{2}{n}+\mathrm{1}}\:=\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{By}\:\mathrm{observing}\:\:\mathrm{the}\:\:\mathrm{pattern},\:\mathrm{we}\:\mathrm{can}\:\mathrm{conjecture}\:\mathrm{a}\:\mathrm{general} \\ $$$$\mathrm{formula}\:{u}_{{n}} \:: \\ $$$$\:\:\:\:\:\:\:{u}_{{n}} \:=\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{Proof}\:\mathrm{by}\:\mathrm{Induction}: \\ $$$$\mathrm{Base}\:\mathrm{case}:\:{u}_{\mathrm{0}} \:=\:\mathrm{3}+\frac{\mathrm{2}}{\mathrm{2}\left(\mathrm{0}\right)+\mathrm{1}}\:=\:\mathrm{5}\: \\ $$$$\mathrm{Assume}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{holds}\:\mathrm{for}\:{n}={k}\:,\:\mathrm{i}.\mathrm{e},\:{u}_{{k}} \:=\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}{k}+\mathrm{1}}\:. \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{holds}\:\mathrm{for}\:{n}\:=\:{k}+\mathrm{1}. \\ $$$$ \\ $$$$\:\:\:{u}_{{k}+\mathrm{1}} \:=\:\frac{\mathrm{4}{u}_{{k}} \:−\:\mathrm{9}}{{u}_{{k}} \:−\:\mathrm{2}}\:=\:\frac{\mathrm{4}\left(\mathrm{3}+\frac{\mathrm{2}}{\mathrm{2}{k}+\mathrm{1}}\right)−\mathrm{9}}{\mathrm{3}+\frac{\mathrm{2}}{\mathrm{2}{k}+\mathrm{1}}\:−\:\mathrm{2}} \\ $$$$\mathrm{Simplifying}\:\mathrm{the}\:\mathrm{expression},\:\mathrm{we}\:\mathrm{get}: \\ $$$$\:\:\:{u}_{{k}+\mathrm{1}} \:=\:\frac{\mathrm{3}\:+\:\frac{\mathrm{8}}{\mathrm{2}{k}+\mathrm{1}}}{\mathrm{1}\:+\:\frac{\mathrm{2}}{\mathrm{2}{k}+\mathrm{1}}}\:=\:\frac{\mathrm{6}{k}+\mathrm{11}}{\mathrm{2}{k}+\mathrm{3}}\:=\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}\left({k}+\mathrm{1}\right)+\mathrm{1}}\: \\ $$$$\mathrm{This}\:\mathrm{matches}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{for}\:{n}\:=\:{k}+\mathrm{1}\:. \\ $$$$ \\ $$$$\mathrm{Therefore},\:\mathrm{the}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the}\:\mathrm{recurrence}\:\mathrm{relation}\:\mathrm{is}: \\ $$$$\:\:\:\:\:\:\:{u}_{{n}} \:=\:\mathrm{3}\:+\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}} \\ $$

Commented by mr W last updated on 13/Dec/24

�� thanks!

Commented by mr W last updated on 13/Dec/24

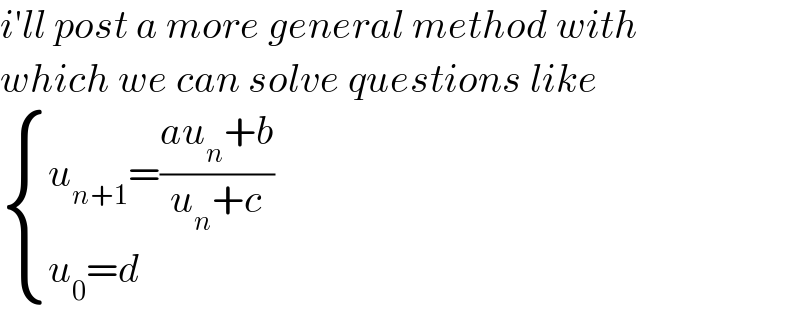
i′ll post a more general method with which we can solve questions like { ((u_(n+1) =((au_n +b)/(u_n +c)))),((u_0 =d)) :}

$${i}'{ll}\:{post}\:{a}\:{more}\:{general}\:{method}\:{with} \\ $$$${which}\:{we}\:{can}\:{solve}\:{questions}\:{like} \\ $$$$\begin{cases}{{u}_{{n}+\mathrm{1}} =\frac{{au}_{{n}} +{b}}{{u}_{{n}} +{c}}}\\{{u}_{\mathrm{0}} ={d}}\end{cases} \\ $$

Answered by mr W last updated on 13/Dec/24

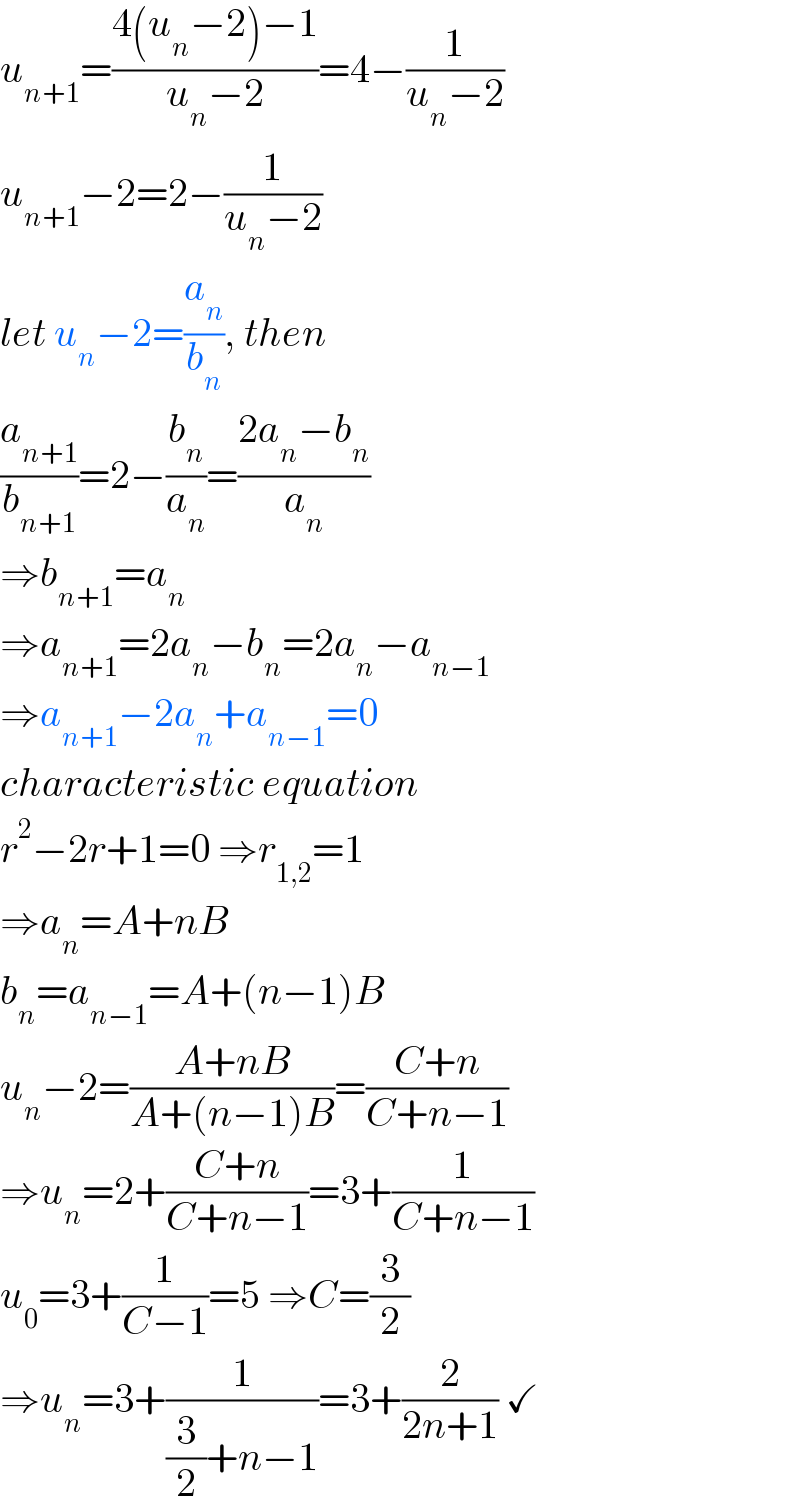
u_(n+1) =((4(u_n −2)−1)/(u_n −2))=4−(1/(u_n −2)) u_(n+1) −2=2−(1/(u_n −2)) let u_n −2=(a_n /b_n ), then (a_(n+1) /b_(n+1) )=2−(b_n /a_n )=((2a_n −b_n )/a_n ) ⇒b_(n+1) =a_n ⇒a_(n+1) =2a_n −b_n =2a_n −a_(n−1) ⇒a_(n+1) −2a_n +a_(n−1) =0 characteristic equation r^2 −2r+1=0 ⇒r_(1,2) =1 ⇒a_n =A+nB b_n =a_(n−1) =A+(n−1)B u_n −2=((A+nB)/(A+(n−1)B))=((C+n)/(C+n−1)) ⇒u_n =2+((C+n)/(C+n−1))=3+(1/(C+n−1)) u_0 =3+(1/(C−1))=5 ⇒C=(3/2) ⇒u_n =3+(1/((3/2)+n−1))=3+(2/(2n+1)) ✓

$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{4}\left({u}_{{n}} −\mathrm{2}\right)−\mathrm{1}}{{u}_{{n}} −\mathrm{2}}=\mathrm{4}−\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{2}} \\ $$$${u}_{{n}+\mathrm{1}} −\mathrm{2}=\mathrm{2}−\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{2}} \\ $$$${let}\:{u}_{{n}} −\mathrm{2}=\frac{{a}_{{n}} }{{b}_{{n}} },\:{then} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} }{{b}_{{n}+\mathrm{1}} }=\mathrm{2}−\frac{{b}_{{n}} }{{a}_{{n}} }=\frac{\mathrm{2}{a}_{{n}} −{b}_{{n}} }{{a}_{{n}} } \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} ={a}_{{n}} \\ $$$$\Rightarrow{a}_{{n}+\mathrm{1}} =\mathrm{2}{a}_{{n}} −{b}_{{n}} =\mathrm{2}{a}_{{n}} −{a}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{a}_{{n}+\mathrm{1}} −\mathrm{2}{a}_{{n}} +{a}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${characteristic}\:{equation} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{1}=\mathrm{0}\:\Rightarrow{r}_{\mathrm{1},\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}} ={A}+{nB} \\ $$$${b}_{{n}} ={a}_{{n}−\mathrm{1}} ={A}+\left({n}−\mathrm{1}\right){B} \\ $$$${u}_{{n}} −\mathrm{2}=\frac{{A}+{nB}}{{A}+\left({n}−\mathrm{1}\right){B}}=\frac{{C}+{n}}{{C}+{n}−\mathrm{1}} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{2}+\frac{{C}+{n}}{{C}+{n}−\mathrm{1}}=\mathrm{3}+\frac{\mathrm{1}}{{C}+{n}−\mathrm{1}} \\ $$$${u}_{\mathrm{0}} =\mathrm{3}+\frac{\mathrm{1}}{{C}−\mathrm{1}}=\mathrm{5}\:\Rightarrow{C}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{3}+\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{2}}+{n}−\mathrm{1}}=\mathrm{3}+\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com