
Question Number 64354 by Rio Michael last updated on 17/Jul/19

$${some}\:{one}\:{write}\:{the}\:{statement} \\ $$$$\:{a}\:\equiv−{a}\left({mod}\:{m}\right)\: \\ $$$${show}\:{that}\:{this}\:{statement}\:{is}\:{not}\:{generally}\:{true}.!\:{giving}\:{a}\:{counter} \\ $$$${example} \\ $$
Answered by MJS last updated on 17/Jul/19

$$\mathrm{49}\boldsymbol{\div}\mathrm{11}= \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{greatest}\:{n}\:\mathrm{with}\:\mathrm{11}{n}\leqslant\mathrm{49}\:\Rightarrow \\ $$$$\Rightarrow\:{n}=\mathrm{4} \\ $$$$\mathrm{49}\boldsymbol{\div}\mathrm{11}=\mathrm{4} \\ $$$$\mathrm{multiplicating}\:``\mathrm{backwards}'' \\ $$$$\mathrm{4}×\mathrm{11}=\mathrm{44} \\ $$$$\mathrm{subtracting} \\ $$$$\:\:\:\:\mathrm{49}\boldsymbol{\div}\mathrm{11}=\mathrm{4} \\ $$$$−\mathrm{44} \\ $$$$=== \\ $$$$\:\:\:\:\:\:\:\mathrm{5}\:\mathrm{remains} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{do}\:\mathrm{the}\:\mathrm{same}\:\mathrm{here}: \\ $$$$\left(−\mathrm{49}\right)\boldsymbol{\div}\mathrm{11}= \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{greatest}\:{n}\:\mathrm{with}\:\mathrm{11}{n}\leqslant\left(−\mathrm{49}\right)\:\Rightarrow \\ $$$$\Rightarrow\:{n}=\left(−\mathrm{5}\right) \\ $$$$\left(−\mathrm{49}\right)\boldsymbol{\div}\mathrm{11}=\left(−\mathrm{5}\right) \\ $$$$\mathrm{multiplicating}\:``\mathrm{backwards}'' \\ $$$$\left(−\mathrm{5}\right)×\mathrm{11}=\left(−\mathrm{55}\right) \\ $$$$\mathrm{subtracting} \\ $$$$\:\:\:\:\:\left(−\mathrm{49}\right)\boldsymbol{\div}\mathrm{11}=\left(−\mathrm{5}\right) \\ $$$$−\left(−\mathrm{55}\right) \\ $$$$===== \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}\:\mathrm{remains} \\ $$$$ \\ $$$$\mathrm{but} \\ $$$$\:\:\:\:\mathrm{49}\boldsymbol{\div}\left(−\mathrm{11}\right)=\left(−\mathrm{4}\right) \\ $$$$−\mathrm{44} \\ $$$$=== \\ $$$$\:\:\:\:\:\:\:\mathrm{5}\:\mathrm{remains} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{for}\:\mathrm{division}\:\mathrm{with}\:\mathrm{remainder}: \\ $$$$\left(−{a}\right):{b}\neq{a}:\left(−{b}\right) \\ $$$$ \\ $$$$\mathrm{remainders}\:\mathrm{are}\:\mathrm{always}\:\geqslant\mathrm{0}\:\mathrm{here} \\ $$$$\mathrm{but}\:\mathrm{some}\:\mathrm{people}\:\mathrm{use}\:\mathrm{different}\:\mathrm{logic}\:\mathrm{which} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{ok}.\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{logic}\:\mathrm{throughout}\:\mathrm{your}\:\mathrm{work} \\ $$
Commented by Rio Michael last updated on 17/Jul/19
$${thank}\:{you}\:{sir} \\ $$
Commented by Rio Michael last updated on 17/Jul/19
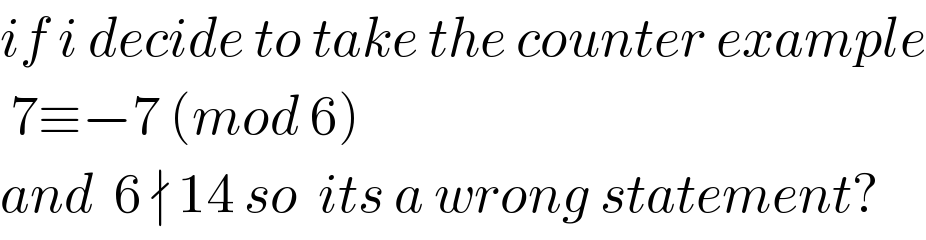
$${if}\:{i}\:{decide}\:{to}\:{take}\:{the}\:{counter}\:{example} \\ $$$$\:\mathrm{7}\equiv−\mathrm{7}\:\left({mod}\:\mathrm{6}\right) \\ $$$${and}\:\:\mathrm{6}\:\nmid\:\mathrm{14}\:{so}\:\:{its}\:{a}\:{wrong}\:{statement}? \\ $$
