Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 96200 by mathmax by abdo last updated on 30/May/20

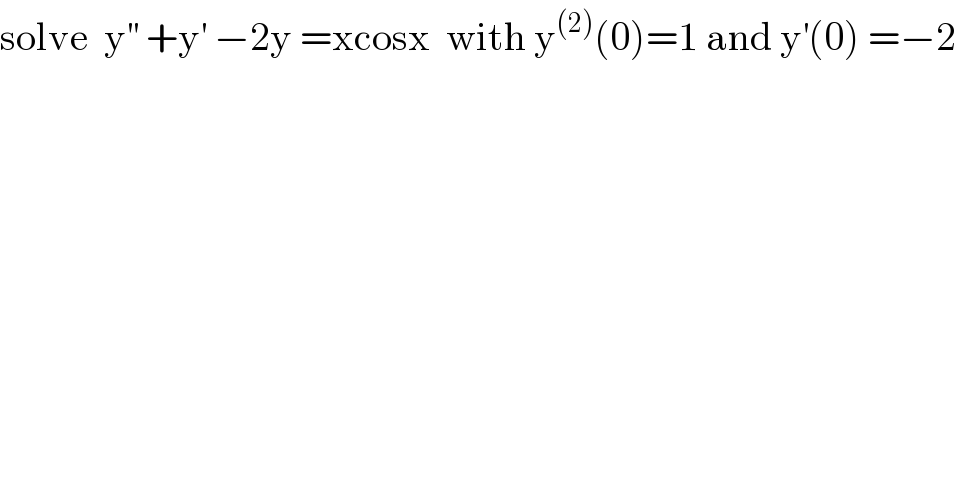
solve y^(′′) +y^′ −2y =xcosx with y^((2)) (0)=1 and y^′ (0) =−2

$$\mathrm{solve}\:\:\mathrm{y}^{''} \:+\mathrm{y}^{'} \:−\mathrm{2y}\:=\mathrm{xcosx}\:\:\mathrm{with}\:\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)\:=−\mathrm{2} \\ $$

Answered by mathmax by abdo last updated on 31/May/20

(he)→r^2 +r−2=0 →Δ =1+8 =9 ⇒r_1 =((−1+3)/2) =1 r_2 =((−1−3)/2) =−2 ⇒y_h =a e^x +b e^(−2x) =au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((u_1 u_2 )),((u_1 ^′ u_2 ^′ )))= determinant (((e^x e^(−2x) )),((e^x −2e^(−2x) )))=−2e^(−x) −e^(−x) =−3e^(−x) W_1 = determinant (((0 e^(−2x) )),((xcosx −2e^(−2x) )))=−x e^(−2x) cosx W_2 = determinant (((e^x 0)),((e^x xcosx)))=x e^x cosx v_1 =∫ (W_1 /W)dx =∫ ((−xe^(−2x) cosx)/(−3e^(−x) ))dx =(1/3)∫ xe^(−x) cosx dx but ∫ xe^(−x) cosx ex =Re(∫ x e^(−x+ix) dx) =Re(∫ xe^((−1+i)x) dx) ∫ xe^((−1+i)x) dx =(x/(−1+i))e^((−1+i)x) −∫ (1/(−1+i))e^((−1+i)x) dx =−(x/(1−i))e^((−1+i)x) +(1/(1−i))×(1/(−1+i)) e^((−1+i)x) =((−x(1+i))/2)e^((−1+i)x) −(1/((1−i)^2 )) e^((−1+i)x) =((−x(1+i))/2)e^((−1+i)x) −(((1+i)^2 )/4) e^((−1+i)x) = =(1/4)e^(−x) (−2x(1+i)(cosx +isinx)−2i(cosx +isinx))=.... v_2 =∫ (W_2 /W)dx =∫ ((xe^x cosx)/(−3e^(−x) ))dx =−(1/3) ∫ xe^(2x) cosx dx =−(1/3)Re(∫ x e^(2x+ix) dx) =−(1/3)(∫ xe^((2+i)x) dx) ∫ x e^((2+i)x) dx =(x/(2+i)) e^((2+i)x) −∫ (1/(2+i)) e^((2+i)x) dx =(x/(2+i))e^((2+x)i) −(1/((2+i)^2 ))e^((2+i)x) =..... y_p =u_1 v_1 +u_2 v_2 and y =y_h +y_p ....be continued...

$$\left(\mathrm{he}\right)\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{r}−\mathrm{2}=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{1}+\mathrm{8}\:=\mathrm{9}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{2}}\:=\mathrm{1} \\ $$$$\mathrm{r}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{3}}{\mathrm{2}}\:=−\mathrm{2}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} ^{'} }\end{vmatrix}=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{2e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} \:=−\mathrm{3e}^{−\mathrm{x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\mathrm{xcosx}\:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cosx} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{xcosx}}\end{vmatrix}=\mathrm{x}\:\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\:\frac{−\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{cosx}}{−\mathrm{3e}^{−\mathrm{x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\:\mathrm{xe}^{−\mathrm{x}} \:\mathrm{cosx}\:\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int\:\:\mathrm{xe}^{−\mathrm{x}} \:\mathrm{cosx}\:\mathrm{ex}\:=\mathrm{Re}\left(\int\:\:\mathrm{x}\:\mathrm{e}^{−\mathrm{x}+\mathrm{ix}} \mathrm{dx}\right)\:=\mathrm{Re}\left(\int\:\:\mathrm{xe}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\right) \\ $$$$\int\:\mathrm{xe}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{x}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:\:−\int\:\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{x}}{\mathrm{1}−\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{i}}×\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \: \\ $$$$=\frac{−\mathrm{x}\left(\mathrm{1}+\mathrm{i}\right)}{\mathrm{2}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:−\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{2}} }\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \\ $$$$=\frac{−\mathrm{x}\left(\mathrm{1}+\mathrm{i}\right)}{\mathrm{2}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:−\frac{\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{4}}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{x}} \left(−\mathrm{2x}\left(\mathrm{1}+\mathrm{i}\right)\left(\mathrm{cosx}\:+\mathrm{isinx}\right)−\mathrm{2i}\left(\mathrm{cosx}\:+\mathrm{isinx}\right)\right)=.... \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{xe}^{\mathrm{x}} \:\mathrm{cosx}}{−\mathrm{3e}^{−\mathrm{x}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\mathrm{xe}^{\mathrm{2x}} \:\mathrm{cosx}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{Re}\left(\int\:\mathrm{x}\:\mathrm{e}^{\mathrm{2x}+\mathrm{ix}} \mathrm{dx}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}}\left(\int\:\mathrm{xe}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx}\right) \\ $$$$\int\:\:\mathrm{x}\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{x}}{\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:−\int\:\frac{\mathrm{1}}{\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{x}}{\mathrm{2}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{2}+\mathrm{x}\right)\mathrm{i}} \:−\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{i}\right)^{\mathrm{2}} }\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:=..... \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} ....\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 31/May/20

let solve by laplace transform (e)⇒L(y^((2)) )+L(y^((1)) )−2L(y) =L(xcosx) ⇒ x^2 L(y)−xy(0)−y^′ (0)+xL(y)−y(o)−2L(y) =L(x cosx) ⇒ (x^2 +x−2)L(y) −(x+1)y(0)+2 =L(xcosx) ⇒ (x^2 +x−2)L(y) =L(xcosx)+(x+1)y(0)−2 ⇒ L(xcosx) =∫_0 ^∞ t cost e^(−xt) dt =Re(∫_0 ^∞ t e^(−xt+it) dt) ∫_0 ^∞ t e^((−x+i)t) dt =[(t/(−x+i)) e^((−x+i)t) ]_0 ^∞ −∫_0 ^∞ (1/(−x+i)) e^((−x+i)t) dt =(1/(x−i))×(1/(−x+i))[ e^((−x+i)t) ]_0 ^∞ =(1/((x−i)^2 )) =(((x+i)^2 )/((x^2 +1)^2 )) =((x^2 +2ix −1)/((x^2 +1)^2 )) ⇒ L(xcosx) =((x^2 −1)/((x^2 +1)^2 )) (e) ⇒(x^2 +x−2)L(y) =((x^2 −1)/((x^2 +1)^2 )) +y(0)(x+1)−2 ⇒ L(y) =((x^2 −1)/((x^2 +1)^2 (x^2 +x−2))) +(((x+1))/(x^2 +x−2))y(0)−(2/(x^2 +x−2)) ⇒ y =L^(−1) (((x^2 −1)/((x^2 +1)^2 (x^2 +x−2))))+y(0)L^(−1) (((x+1)/(x^2 +x−2))) −2 L^(−1) ((1/(x^2 +x−2))) x^2 +x−2 =x^2 −1 +x−1 =(x−1)(x+1)+x−1 =(x−1)(x+2) ⇒ (1/(x^2 +x−2)) =(1/((x−1)(x+2))) =(1/3)((1/(x−1))−(1/(x+2))) ⇒ L^(−1) ((1/(x^2 +x−2))) =(1/3)L^(−1) ((1/(x−1)))−(1/3)L^(−1) ((1/(x+2))) =(1/3)e^x −(1/3)e^(−2x) ((x+1)/(x^2 +x−2)) =((x+1)/3)((1/(x−1))−(1/(x+2))) =(1/3)×((x+1)/(x−1))−(1/3)×((x+1)/(x+2)) =(1/3)×((x−1+2)/(x−1)) −(1/3)×((x+2−1)/(x+2)) =(1/3) +(2/(3(x−1)))−(1/3) +(1/(3(x+2))) ⇒L^(−1) (((x+1)/(x^2 +x−2))) =(2/3)e^x +(1/3)e^(−2x) we have ((x^2 −1)/((x^2 +1)^2 (x^2 +x+2))) =(((x−1)(x+1))/((x^2 +1)^2 (x−1)(x+2))) =((x+1)/((x+2)(x^2 +1)^2 )) =(a/(x+2)) +((bx +c)/(x^2 +1)) +((dx +e)/((x^2 +1)^2 )) ⇒L^(−1) (....) =aL^(−1) ((1/(x+2))) +bL^(−1) ((x/(x^2 +1))) +cL^(−1) ((1/(x^2 +1)))+dL^(−1) ((x/((x^2 +1)^2 )))+eL^(−1) ((1/((x^2 +1)^2 )))p =a e^(−2x) +bcosx +c sinx +d L^(−1) ((x/((x^2 +1)^2 )))+.... ....be continued...

$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{L}\left(\mathrm{y}^{\left(\mathrm{2}\right)} \right)+\mathrm{L}\left(\mathrm{y}^{\left(\mathrm{1}\right)} \right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{xcosx}\right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)+\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{o}\right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{x}\:\mathrm{cosx}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}\left(\mathrm{0}\right)+\mathrm{2}\:=\mathrm{L}\left(\mathrm{xcosx}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{xcosx}\right)+\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}\left(\mathrm{0}\right)−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{xcosx}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{cost}\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\mathrm{xt}+\mathrm{it}} \mathrm{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{t}}{−\mathrm{x}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}×\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\left[\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} }\:=\frac{\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2ix}\:−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{xcosx}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{e}\right)\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\mathrm{y}\left(\mathrm{0}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)}\:+\frac{\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\mathrm{y}\left(\mathrm{0}\right)−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)}\right)+\mathrm{y}\left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\right)\:−\mathrm{2}\:\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:+\mathrm{x}−\mathrm{1}\:=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{x}−\mathrm{1}\:=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}}\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{2x}} \\ $$$$\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}}\:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}+\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{x}−\mathrm{1}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{x}+\mathrm{2}−\mathrm{1}}{\mathrm{x}+\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\Rightarrow\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}}\right)\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{2}\right)}\:=\frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:=\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{2}}\:+\frac{\mathrm{bx}\:+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\:+\frac{\mathrm{dx}\:+\mathrm{e}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{L}^{−\mathrm{1}} \left(....\right) \\ $$$$=\mathrm{aL}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:+\mathrm{bL}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\:+\mathrm{cL}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)+\mathrm{dL}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\right)+\mathrm{eL}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{p} \\ $$$$=\mathrm{a}\:\mathrm{e}^{−\mathrm{2x}} \:+\mathrm{bcosx}\:+\mathrm{c}\:\mathrm{sinx}\:+\mathrm{d}\:\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\right)+.... \\ $$$$....\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com