
Previous in Relation and Functions Next in Relation and Functions
Question Number 143259 by Mathspace last updated on 12/Jun/21
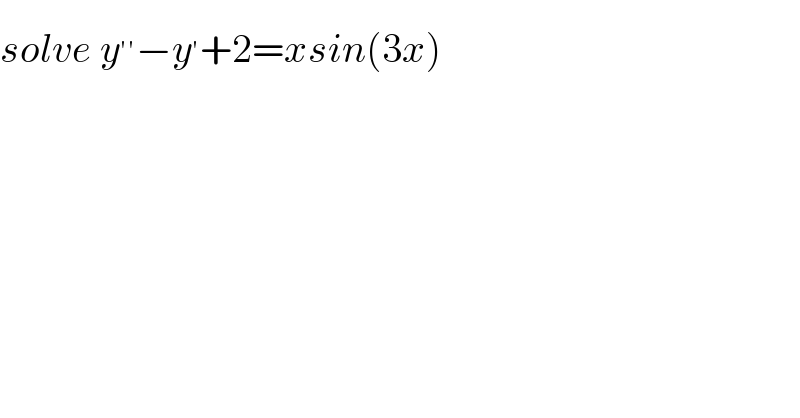
$${solve}\:{y}^{''} −{y}^{'} +\mathrm{2}={xsin}\left(\mathrm{3}{x}\right) \\ $$
Answered by qaz last updated on 12/Jun/21
![y_p =(1/(D^2 −D))[xsin (3x)−2] =(1/(D−1))(−(1/3)xcos 3x+(1/9)sin 3x−2x) =−(1/3)∙(1/(D−1))(xcos 3x)+(1/9)∙(1/(D−1))(sin 3x)+2x+2 =−(1/3)(x−(1/(D−1)))(1/(D−1))cos 3x+(1/9)∙((D+1)/((−3^2 )−1))sin 3x+2x+2 =−(1/3)(x−(1/(D−1)))((D+1)/((−3^2 )−1))cos 3x−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))(x−(1/(D−1)))(−3sin 3x+cos 3x)−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x+((1+D)/(10))(−3sin 3x+cos 3x)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x−((4cos 3x+3sin 3x)/5)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =−(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x+2 ⇒y=C_1 +C_2 e^x −(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x −−−−−−−−−−−−−−−−−−− y_p =(1/(D^2 −D))(xsin 3x−2) =(x−((2D−1)/(D^2 −D)))(1/(D^2 −D))(sin 3x)−(1/(D−1))(2x) =(x−((2D−1)/(D^2 −D)))((D^2 +D)/((−3^2 )^2 −(−3^2 )))(sin 3x)+2x+2 =(1/(90))(x−((2D−1)/(D^2 −D)))(3cos 3x−9sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙((2D−1)/(D^2 −D))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙(((2D−1)(D^2 +D))/((−3^2 )^2 −(−3^2 )))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(2D−1)(4sin 3x−3cos 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x+2 ⇒y=C_1 +C_2 e^x +(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x](Q143291.png)
$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\left[\mathrm{xsin}\:\left(\mathrm{3x}\right)−\mathrm{2}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{xcos}\:\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{sin}\:\mathrm{3x}−\mathrm{2x}\right) \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\left(\mathrm{xcos}\:\mathrm{3x}\right)+\frac{\mathrm{1}}{\mathrm{9}}\centerdot\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\left(\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\right)\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\mathrm{cos}\:\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{9}}\centerdot\frac{\mathrm{D}+\mathrm{1}}{\left(−\mathrm{3}^{\mathrm{2}} \right)−\mathrm{1}}\mathrm{sin}\:\mathrm{3x}+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\right)\frac{\mathrm{D}+\mathrm{1}}{\left(−\mathrm{3}^{\mathrm{2}} \right)−\mathrm{1}}\mathrm{cos}\:\mathrm{3x}−\frac{\mathrm{1}}{\mathrm{90}}\left(\mathrm{3cos}\:\mathrm{3x}+\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\right)\left(−\mathrm{3sin}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{90}}\left(\mathrm{3cos}\:\mathrm{3x}+\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{30}}\left[−\mathrm{3xsin}\:\mathrm{3x}+\mathrm{xcos}\:\mathrm{3x}+\frac{\mathrm{1}+\mathrm{D}}{\mathrm{10}}\left(−\mathrm{3sin}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{3x}\right)\right]−\frac{\mathrm{1}}{\mathrm{90}}\left(\mathrm{3cos}\:\mathrm{3x}+\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{30}}\left[−\mathrm{3xsin}\:\mathrm{3x}+\mathrm{xcos}\:\mathrm{3x}−\frac{\mathrm{4cos}\:\mathrm{3x}+\mathrm{3sin}\:\mathrm{3x}}{\mathrm{5}}\right]−\frac{\mathrm{1}}{\mathrm{90}}\left(\mathrm{3cos}\:\mathrm{3x}+\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{10}}\mathrm{xsin}\:\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{30}}\mathrm{xcos}\:\mathrm{3x}−\frac{\mathrm{3}}{\mathrm{50}}\mathrm{cos}\:\mathrm{3x}−\frac{\mathrm{7}}{\mathrm{225}}\mathrm{sin}\:\mathrm{3x}+\mathrm{2x}+\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} −\frac{\mathrm{1}}{\mathrm{10}}\mathrm{xsin}\:\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{30}}\mathrm{xcos}\:\mathrm{3x}−\frac{\mathrm{3}}{\mathrm{50}}\mathrm{cos}\:\mathrm{3x}−\frac{\mathrm{7}}{\mathrm{225}}\mathrm{sin}\:\mathrm{3x}+\mathrm{2x} \\ $$$$−−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\left(\mathrm{xsin}\:\mathrm{3x}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\left(\mathrm{x}−\frac{\mathrm{2D}−\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\right)\frac{\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\left(\mathrm{sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{D}−\mathrm{1}}\left(\mathrm{2x}\right) \\ $$$$\:\:\:\:\:=\left(\mathrm{x}−\frac{\mathrm{2D}−\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\right)\frac{\mathrm{D}^{\mathrm{2}} +\mathrm{D}}{\left(−\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(−\mathrm{3}^{\mathrm{2}} \right)}\left(\mathrm{sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{90}}\left(\mathrm{x}−\frac{\mathrm{2D}−\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\right)\left(\mathrm{3cos}\:\mathrm{3x}−\mathrm{9sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{x}}{\mathrm{30}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{30}}\centerdot\frac{\mathrm{2D}−\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{D}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{x}}{\mathrm{30}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{30}}\centerdot\frac{\left(\mathrm{2D}−\mathrm{1}\right)\left(\mathrm{D}^{\mathrm{2}} +\mathrm{D}\right)}{\left(−\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(−\mathrm{3}^{\mathrm{2}} \right)}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{x}}{\mathrm{30}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{450}}\left(\mathrm{2D}−\mathrm{1}\right)\left(\mathrm{4sin}\:\mathrm{3x}−\mathrm{3cos}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\:\:\:\:\:=\frac{\mathrm{x}}{\mathrm{30}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{450}}\left(\mathrm{27cos}\:\mathrm{3x}+\mathrm{14sin}\:\mathrm{3x}\right)+\mathrm{2x}+\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{x}} +\frac{\mathrm{x}}{\mathrm{30}}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{3sin}\:\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{450}}\left(\mathrm{27cos}\:\mathrm{3x}+\mathrm{14sin}\:\mathrm{3x}\right)+\mathrm{2x} \\ $$
