
Previous in Relation and Functions Next in Relation and Functions
Question Number 98657 by mathmax by abdo last updated on 15/Jun/20
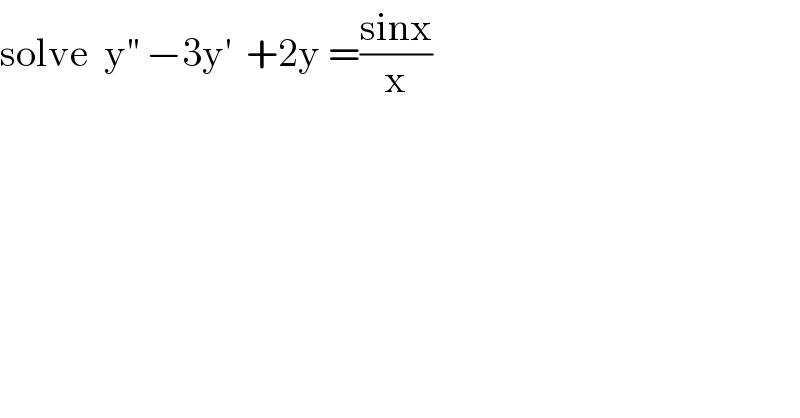
$$\mathrm{solve}\:\:\mathrm{y}^{''} \:−\mathrm{3y}^{'} \:\:+\mathrm{2y}\:=\frac{\mathrm{sinx}}{\mathrm{x}} \\ $$
Answered by maths mind last updated on 15/Jun/20
![y′′−3y′+2y=0 ⇒y=ae^x +be^(2x) let y=ke^x particular sokution ⇒y′=(k′+k)e^x ,y′′=(k′′+2k′+k)e^x ⇒ (k′′−k′)e^x =((sin(x))/x) ⇒k′′−k′=((sin(x)e^(−x) )/x)=Im{(e^((i−1)x) /x)} k′−k=∫(e^((i−1)x) /x)dx=∫(e^u /u)du=Ei(u)=Ei((i−1)x) ⇒k′−k=E_i ((i−1)x) k=se^x ⇒s′=∫e^(−x) E_i ((i−1)x) =[−e^(−x) E_i (i−1)x)]+∫e^(−x) .(e^((i−1)x) /x)dx =E_i ((i−2)x) k=e^x E_i ((i−2)x)) Y_p =Im{e^(2x) E_i ((i−2)x))} e^(2x) Im{∫_(−∞) ^x (e^((i−2)x) /x)dx} =e^(2x) Im{∫((e^(−2x) (cos(x)+isin(x)))/x)dx} =e^(2x) [((E_i ((i−2)x)−E_i ((−i−2)x))/(2i))] S=ae^x +be^(2x) +e^(2x) [((E_i ((i−2)x)−E_i ((−i−2)x))/(2i))]](Q98693.png)
$${y}''−\mathrm{3}{y}'+\mathrm{2}{y}=\mathrm{0} \\ $$$$\Rightarrow{y}={ae}^{{x}} +{be}^{\mathrm{2}{x}} \\ $$$${let}\:{y}={ke}^{{x}} {particular}\:{sokution} \\ $$$$\Rightarrow{y}'=\left({k}'+{k}\right){e}^{{x}} ,{y}''=\left({k}''+\mathrm{2}{k}'+{k}\right){e}^{{x}} \Rightarrow \\ $$$$\left({k}''−{k}'\right){e}^{{x}} =\frac{{sin}\left({x}\right)}{{x}} \\ $$$$\Rightarrow{k}''−{k}'=\frac{{sin}\left({x}\right){e}^{−{x}} }{{x}}={Im}\left\{\frac{{e}^{\left({i}−\mathrm{1}\right){x}} }{{x}}\right\} \\ $$$${k}'−{k}=\int\frac{{e}^{\left({i}−\mathrm{1}\right){x}} }{{x}}{dx}=\int\frac{{e}^{{u}} }{{u}}{du}={Ei}\left({u}\right)={Ei}\left(\left({i}−\mathrm{1}\right){x}\right) \\ $$$$\Rightarrow{k}'−{k}={E}_{{i}} \left(\left({i}−\mathrm{1}\right){x}\right) \\ $$$${k}={se}^{{x}} \Rightarrow{s}'=\int{e}^{−{x}} {E}_{{i}} \left(\left({i}−\mathrm{1}\right){x}\right) \\ $$$$\left.=\left[−{e}^{−{x}} {E}_{{i}} \left({i}−\mathrm{1}\right){x}\right)\right]+\int{e}^{−{x}} .\frac{{e}^{\left({i}−\mathrm{1}\right){x}} }{{x}}{dx} \\ $$$$={E}_{{i}} \left(\left({i}−\mathrm{2}\right){x}\right) \\ $$$$\left.{k}={e}^{{x}} {E}_{{i}} \left(\left({i}−\mathrm{2}\right){x}\right)\right) \\ $$$$\left.{Y}_{{p}} ={Im}\left\{{e}^{\mathrm{2}{x}} {E}_{{i}} \left(\left({i}−\mathrm{2}\right){x}\right)\right)\right\} \\ $$$${e}^{\mathrm{2}{x}} {Im}\left\{\int_{−\infty} ^{{x}} \frac{{e}^{\left({i}−\mathrm{2}\right){x}} }{{x}}{dx}\right\} \\ $$$$={e}^{\mathrm{2}{x}} {Im}\left\{\int\frac{{e}^{−\mathrm{2}{x}} \left({cos}\left({x}\right)+{isin}\left({x}\right)\right)}{{x}}{dx}\right\} \\ $$$$={e}^{\mathrm{2}{x}} \left[\frac{{E}_{{i}} \left(\left({i}−\mathrm{2}\right){x}\right)−{E}_{{i}} \left(\left(−{i}−\mathrm{2}\right){x}\right)}{\mathrm{2}{i}}\right] \\ $$$${S}={ae}^{{x}} +{be}^{\mathrm{2}{x}} +{e}^{\mathrm{2}{x}} \left[\frac{{E}_{{i}} \left(\left({i}−\mathrm{2}\right){x}\right)−{E}_{{i}} \left(\left(−{i}−\mathrm{2}\right){x}\right)}{\mathrm{2}{i}}\right] \\ $$
Commented by mathmax by abdo last updated on 15/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20
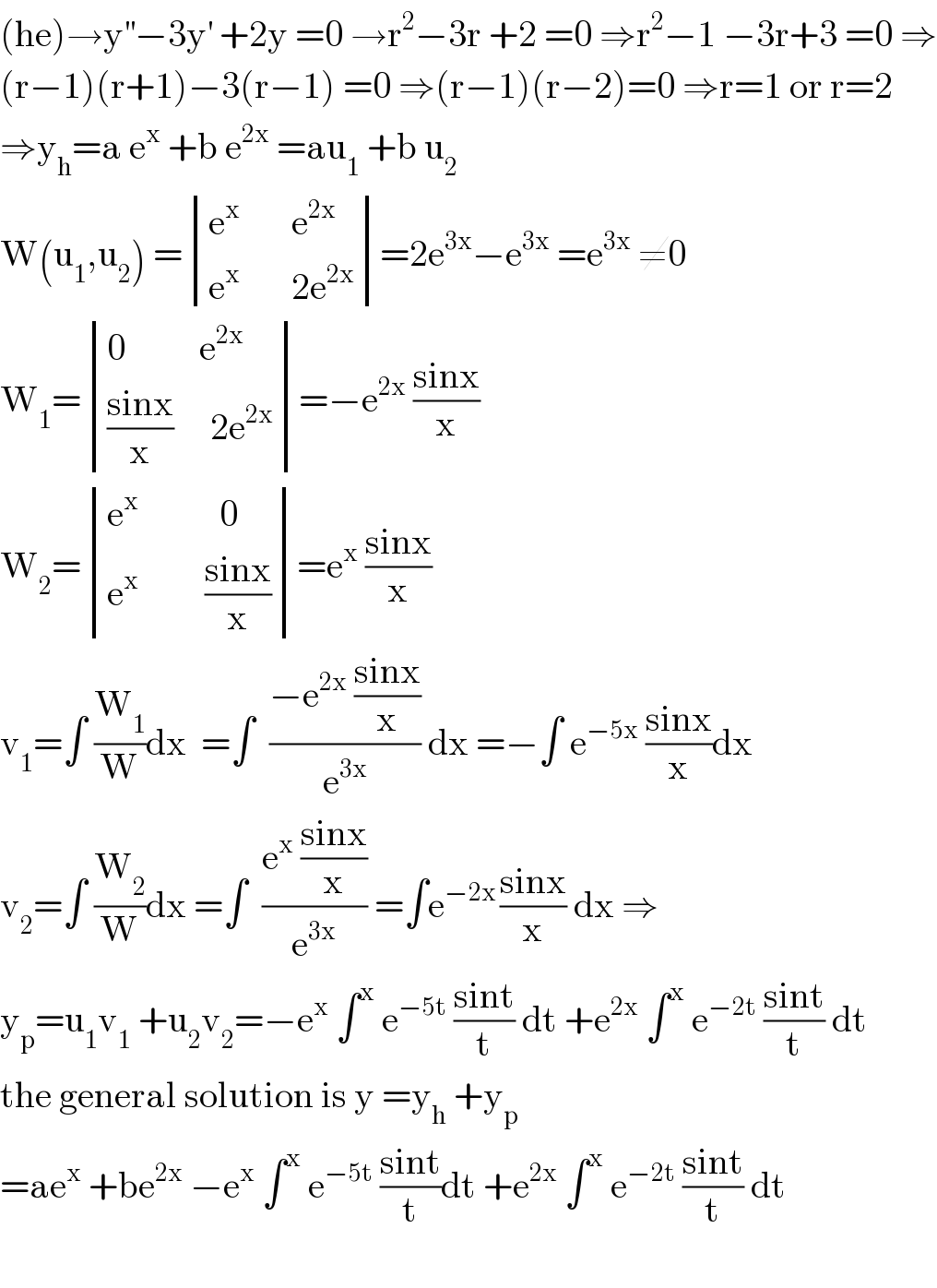
$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} −\mathrm{3y}^{'} \:+\mathrm{2y}\:=\mathrm{0}\:\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{3r}\:+\mathrm{2}\:=\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{1}\:−\mathrm{3r}+\mathrm{3}\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{r}−\mathrm{1}\right)\left(\mathrm{r}+\mathrm{1}\right)−\mathrm{3}\left(\mathrm{r}−\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow\left(\mathrm{r}−\mathrm{1}\right)\left(\mathrm{r}−\mathrm{2}\right)=\mathrm{0}\:\Rightarrow\mathrm{r}=\mathrm{1}\:\mathrm{or}\:\mathrm{r}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{b}\:\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{2e}^{\mathrm{3x}} −\mathrm{e}^{\mathrm{3x}} \:=\mathrm{e}^{\mathrm{3x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\frac{\mathrm{sinx}}{\mathrm{x}}\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\mathrm{e}^{\mathrm{2x}} \:\frac{\mathrm{sinx}}{\mathrm{x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\frac{\mathrm{sinx}}{\mathrm{x}}}\end{vmatrix}=\mathrm{e}^{\mathrm{x}} \:\frac{\mathrm{sinx}}{\mathrm{x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:\:=\int\:\:\frac{−\mathrm{e}^{\mathrm{2x}} \:\frac{\mathrm{sinx}}{\mathrm{x}}}{\mathrm{e}^{\mathrm{3x}} }\:\mathrm{dx}\:=−\int\:\mathrm{e}^{−\mathrm{5x}} \:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{e}^{\mathrm{x}} \:\frac{\mathrm{sinx}}{\mathrm{x}}}{\mathrm{e}^{\mathrm{3x}} }\:=\int\mathrm{e}^{−\mathrm{2x}\:} \frac{\mathrm{sinx}}{\mathrm{x}}\:\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\mathrm{e}^{\mathrm{x}} \:\int^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{5t}} \:\frac{\mathrm{sint}}{\mathrm{t}}\:\mathrm{dt}\:+\mathrm{e}^{\mathrm{2x}} \:\int^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{2t}} \:\frac{\mathrm{sint}}{\mathrm{t}}\:\mathrm{dt} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{2x}} \:−\mathrm{e}^{\mathrm{x}} \:\int^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{5t}} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}\:+\mathrm{e}^{\mathrm{2x}} \:\int^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{2t}} \:\frac{\mathrm{sint}}{\mathrm{t}}\:\mathrm{dt} \\ $$$$ \\ $$
