
Previous in Relation and Functions Next in Relation and Functions
Question Number 97626 by mathmax by abdo last updated on 08/Jun/20
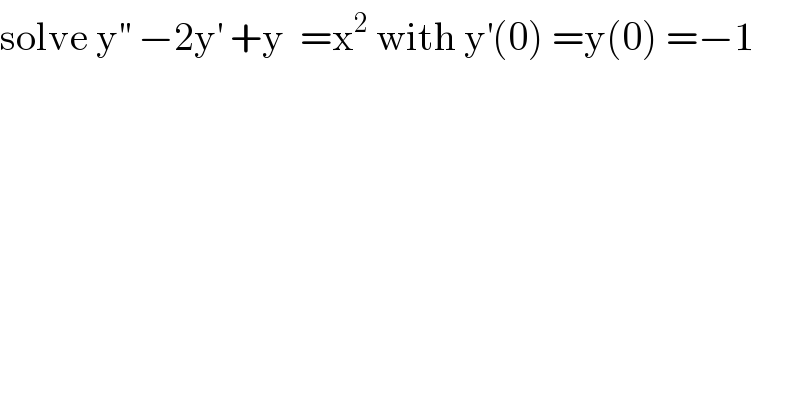
$$\mathrm{solve}\:\mathrm{y}^{''} \:−\mathrm{2y}^{'} \:+\mathrm{y}\:\:=\mathrm{x}^{\mathrm{2}} \:\mathrm{with}\:\mathrm{y}^{'} \left(\mathrm{0}\right)\:=\mathrm{y}\left(\mathrm{0}\right)\:=−\mathrm{1} \\ $$
Commented by bemath last updated on 09/Jun/20
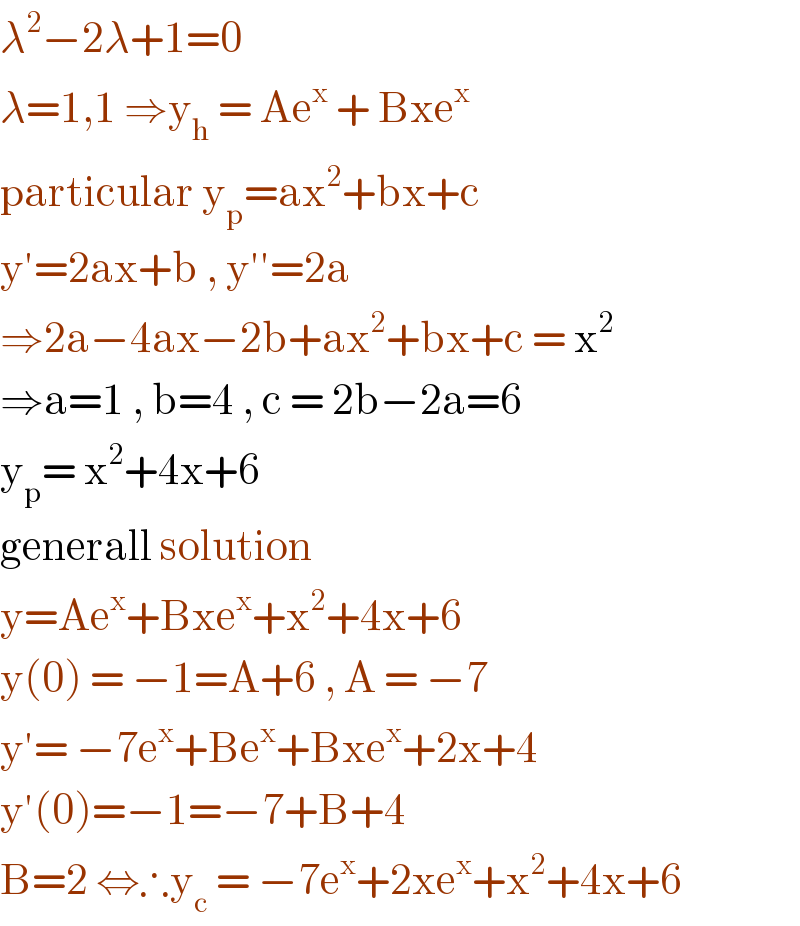
$$\lambda^{\mathrm{2}} −\mathrm{2}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\mathrm{1},\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{\mathrm{x}} \:+\:\mathrm{Bxe}^{\mathrm{x}} \\ $$$$\mathrm{particular}\:\mathrm{y}_{\mathrm{p}} =\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c} \\ $$$$\mathrm{y}'=\mathrm{2ax}+\mathrm{b}\:,\:\mathrm{y}''=\mathrm{2a} \\ $$$$\Rightarrow\mathrm{2a}−\mathrm{4ax}−\mathrm{2b}+\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\:=\:\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{1}\:,\:\mathrm{b}=\mathrm{4}\:,\:\mathrm{c}\:=\:\mathrm{2b}−\mathrm{2a}=\mathrm{6} \\ $$$$\mathrm{y}_{\mathrm{p}} =\:\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{6}\: \\ $$$$\mathrm{generall}\:\mathrm{solution}\: \\ $$$$\mathrm{y}=\mathrm{Ae}^{\mathrm{x}} +\mathrm{Bxe}^{\mathrm{x}} +\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{6} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)\:=\:−\mathrm{1}=\mathrm{A}+\mathrm{6}\:,\:\mathrm{A}\:=\:−\mathrm{7} \\ $$$$\mathrm{y}'=\:−\mathrm{7e}^{\mathrm{x}} +\mathrm{Be}^{\mathrm{x}} +\mathrm{Bxe}^{\mathrm{x}} +\mathrm{2x}+\mathrm{4} \\ $$$$\mathrm{y}'\left(\mathrm{0}\right)=−\mathrm{1}=−\mathrm{7}+\mathrm{B}+\mathrm{4} \\ $$$$\mathrm{B}=\mathrm{2}\:\Leftrightarrow\therefore\mathrm{y}_{\mathrm{c}} \:=\:−\mathrm{7e}^{\mathrm{x}} +\mathrm{2xe}^{\mathrm{x}} +\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{6} \\ $$
Commented by bobhans last updated on 09/Jun/20

$$\mathrm{good} \\ $$
