
Previous in Relation and Functions Next in Relation and Functions
Question Number 57414 by Abdo msup. last updated on 03/Apr/19
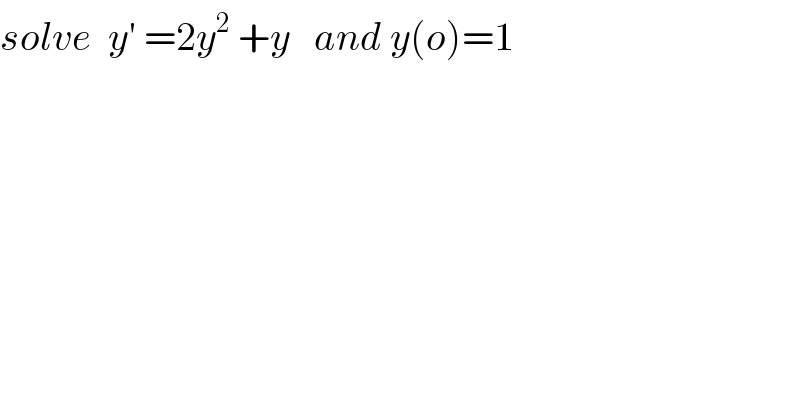
$${solve}\:\:{y}'\:=\mathrm{2}{y}^{\mathrm{2}} \:+{y}\:\:\:{and}\:{y}\left({o}\right)=\mathrm{1} \\ $$
Commented by kaivan.ahmadi last updated on 03/Apr/19
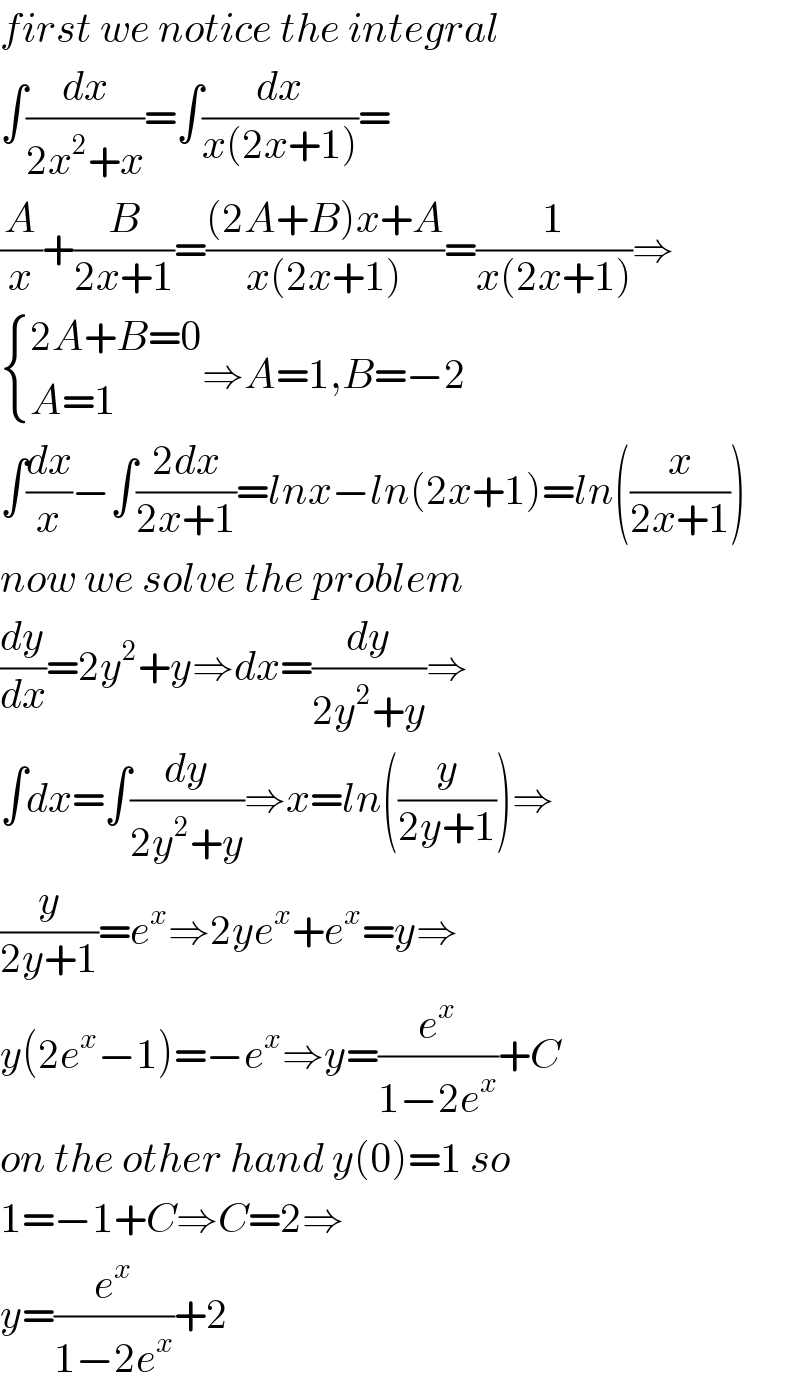
$${first}\:{we}\:{notice}\:{the}\:{integral} \\ $$$$\int\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +{x}}=\int\frac{{dx}}{{x}\left(\mathrm{2}{x}+\mathrm{1}\right)}= \\ $$$$\frac{{A}}{{x}}+\frac{{B}}{\mathrm{2}{x}+\mathrm{1}}=\frac{\left(\mathrm{2}{A}+{B}\right){x}+{A}}{{x}\left(\mathrm{2}{x}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}\left(\mathrm{2}{x}+\mathrm{1}\right)}\Rightarrow \\ $$$$\begin{cases}{\mathrm{2}{A}+{B}=\mathrm{0}}\\{{A}=\mathrm{1}}\end{cases}\Rightarrow{A}=\mathrm{1},{B}=−\mathrm{2} \\ $$$$\int\frac{{dx}}{{x}}−\int\frac{\mathrm{2}{dx}}{\mathrm{2}{x}+\mathrm{1}}={lnx}−{ln}\left(\mathrm{2}{x}+\mathrm{1}\right)={ln}\left(\frac{{x}}{\mathrm{2}{x}+\mathrm{1}}\right) \\ $$$${now}\:{we}\:{solve}\:{the}\:{problem} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{y}^{\mathrm{2}} +{y}\Rightarrow{dx}=\frac{{dy}}{\mathrm{2}{y}^{\mathrm{2}} +{y}}\Rightarrow \\ $$$$\int{dx}=\int\frac{{dy}}{\mathrm{2}{y}^{\mathrm{2}} +{y}}\Rightarrow{x}={ln}\left(\frac{{y}}{\mathrm{2}{y}+\mathrm{1}}\right)\Rightarrow \\ $$$$\frac{{y}}{\mathrm{2}{y}+\mathrm{1}}={e}^{{x}} \Rightarrow\mathrm{2}{ye}^{{x}} +{e}^{{x}} ={y}\Rightarrow \\ $$$${y}\left(\mathrm{2}{e}^{{x}} −\mathrm{1}\right)=−{e}^{{x}} \Rightarrow{y}=\frac{{e}^{{x}} }{\mathrm{1}−\mathrm{2}{e}^{{x}} }+{C} \\ $$$${on}\:{the}\:{other}\:{hand}\:{y}\left(\mathrm{0}\right)=\mathrm{1}\:{so} \\ $$$$\mathrm{1}=−\mathrm{1}+{C}\Rightarrow{C}=\mathrm{2}\Rightarrow \\ $$$${y}=\frac{{e}^{{x}} }{\mathrm{1}−\mathrm{2}{e}^{{x}} }+\mathrm{2} \\ $$
Commented by maxmathsup by imad last updated on 04/Apr/19
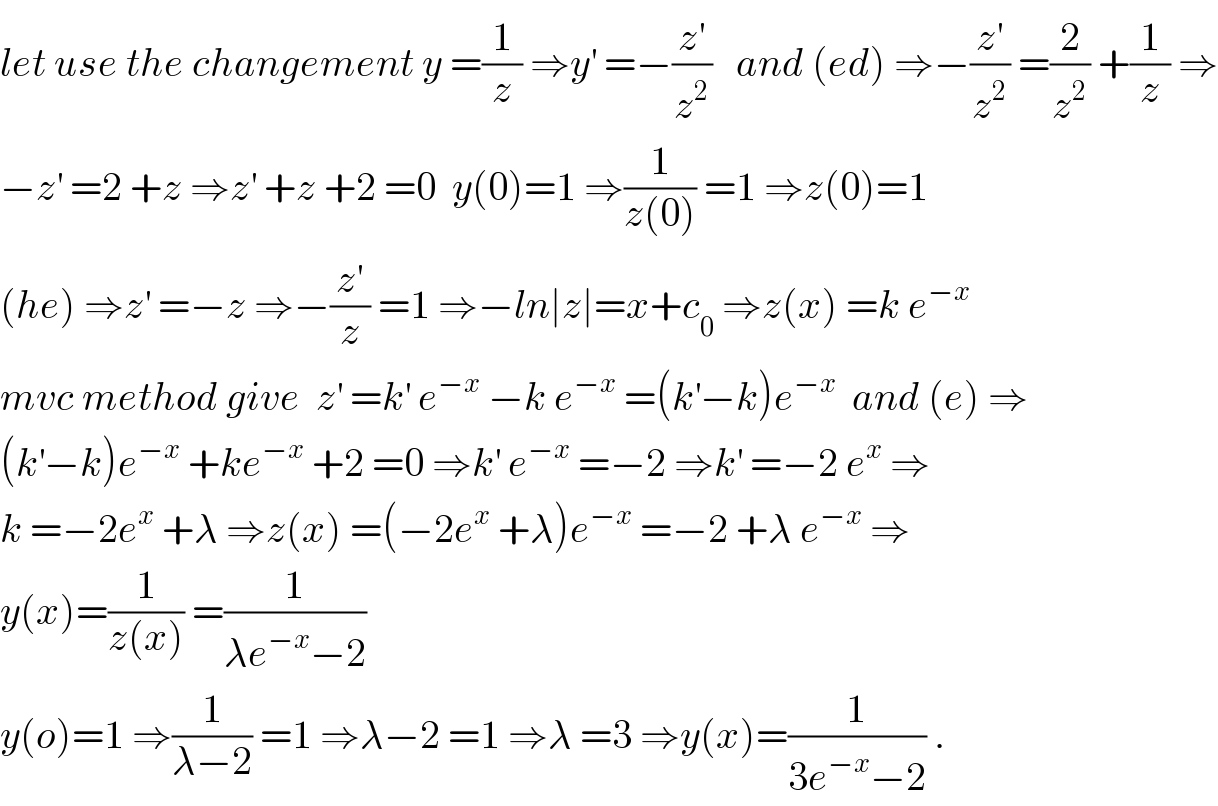
$${let}\:{use}\:{the}\:{changement}\:{y}\:=\frac{\mathrm{1}}{{z}}\:\Rightarrow{y}^{'} \:=−\frac{{z}^{'} }{{z}^{\mathrm{2}} }\:\:\:{and}\:\left({ed}\right)\:\Rightarrow−\frac{{z}^{'} }{{z}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{{z}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{z}}\:\Rightarrow \\ $$$$−{z}^{'} \:=\mathrm{2}\:+{z}\:\Rightarrow{z}^{'} \:+{z}\:+\mathrm{2}\:=\mathrm{0}\:\:{y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{{z}\left(\mathrm{0}\right)}\:=\mathrm{1}\:\Rightarrow{z}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\left({he}\right)\:\Rightarrow{z}^{'} \:=−{z}\:\Rightarrow−\frac{{z}^{'} }{{z}}\:=\mathrm{1}\:\Rightarrow−{ln}\mid{z}\mid={x}+{c}_{\mathrm{0}} \:\Rightarrow{z}\left({x}\right)\:={k}\:{e}^{−{x}} \: \\ $$$${mvc}\:{method}\:{give}\:\:{z}^{'} \:={k}^{'} \:{e}^{−{x}} \:−{k}\:{e}^{−{x}} \:=\left({k}^{'} −{k}\right){e}^{−{x}} \:\:{and}\:\left({e}\right)\:\Rightarrow \\ $$$$\left({k}^{'} −{k}\right){e}^{−{x}} \:+{ke}^{−{x}} \:+\mathrm{2}\:=\mathrm{0}\:\Rightarrow{k}^{'} \:{e}^{−{x}} \:=−\mathrm{2}\:\Rightarrow{k}^{'} \:=−\mathrm{2}\:{e}^{{x}} \:\Rightarrow \\ $$$${k}\:=−\mathrm{2}{e}^{{x}} \:+\lambda\:\Rightarrow{z}\left({x}\right)\:=\left(−\mathrm{2}{e}^{{x}} \:+\lambda\right){e}^{−{x}} \:=−\mathrm{2}\:+\lambda\:{e}^{−{x}} \:\Rightarrow \\ $$$${y}\left({x}\right)=\frac{\mathrm{1}}{{z}\left({x}\right)}\:=\frac{\mathrm{1}}{\lambda{e}^{−{x}} −\mathrm{2}} \\ $$$${y}\left({o}\right)=\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\lambda−\mathrm{2}}\:=\mathrm{1}\:\Rightarrow\lambda−\mathrm{2}\:=\mathrm{1}\:\Rightarrow\lambda\:=\mathrm{3}\:\Rightarrow{y}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}{e}^{−{x}} −\mathrm{2}}\:. \\ $$
