
Question Number 115367 by Bird last updated on 25/Sep/20
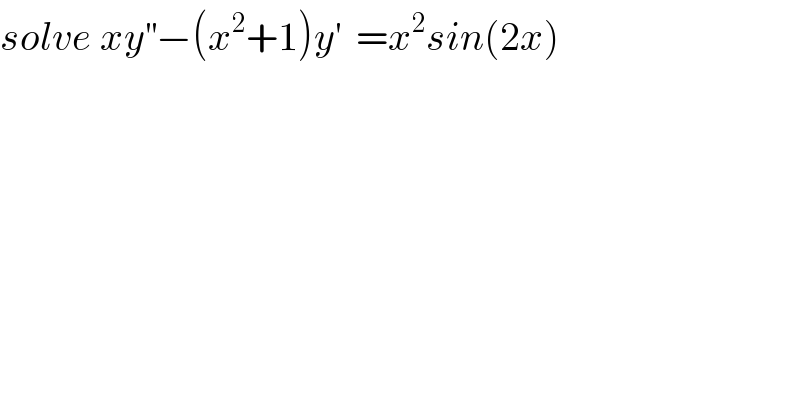
$${solve}\:{xy}^{''} −\left({x}^{\mathrm{2}} +\mathrm{1}\right){y}^{'} \:\:={x}^{\mathrm{2}} {sin}\left(\mathrm{2}{x}\right) \\ $$
Answered by Olaf last updated on 26/Sep/20

$$ \\ $$$${xy}''−\left({x}^{\mathrm{2}} +\mathrm{1}\right){y}'\:=\:{x}^{\mathrm{2}} \mathrm{sin2}{x} \\ $$$$\mathrm{Let}\:{u}\:=\:\frac{{y}'}{{x}} \\ $$$${y}''\:=\:{xu}'+{u} \\ $$$${x}\left({xu}'+{u}\right)−\left({x}^{\mathrm{2}} +\mathrm{1}\right){xu}\:=\:{x}^{\mathrm{2}} \mathrm{sin2}{x} \\ $$$${xu}'+{u}−\left({x}^{\mathrm{2}} +\mathrm{1}\right){u}\:=\:{x}\mathrm{sin2}{x} \\ $$$${xu}'−{x}^{\mathrm{2}} {u}\:=\:{x}\mathrm{sin2}{x} \\ $$$${u}'−{xu}\:=\:\mathrm{sin2}{x} \\ $$$${e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {u}'−{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {u}\:=\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}} \\ $$$$\Rightarrow\:\mathrm{Integration}\:\mathrm{by}\:\mathrm{parts}. \\ $$$$\mathrm{The}\:\mathrm{function}\:{u}\:\mathrm{is}\:\mathrm{a}\:\mathrm{linear}\:\mathrm{combination} \\ $$$$\mathrm{of}\:\mathrm{functions}\:\mathrm{erf}. \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{expression}\:! \\ $$
