
Previous in Relation and Functions Next in Relation and Functions
Question Number 90973 by abdomathmax last updated on 27/Apr/20
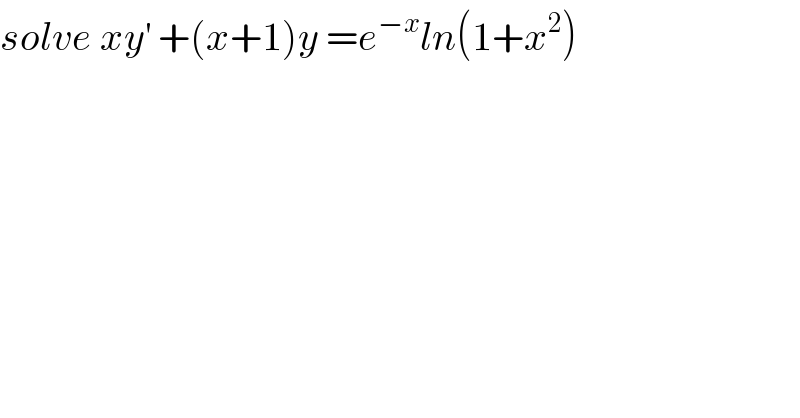
$${solve}\:{xy}^{'} \:+\left({x}+\mathrm{1}\right){y}\:={e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$
Commented by mathmax by abdo last updated on 27/Apr/20
![(he)→xy^′ +(x+1)y =0 ⇒xy^′ =−(x+1)y ⇒(y^′ /y)=−((x+1)/x) =−1−(1/x) ⇒ln∣y∣ =−x−ln∣x∣ +c ⇒y(x)=k e^(−x) ×(1/(∣x∣)) solution on ]0,+∞[ ⇒y(x) =k (e^(−x) /x) let use mvc method y^′ =k^′ (e^(−x) /x) +k{−(1/x^2 )e^(−x) −(1/x)e^(−x) } (e)⇒k^′ e^(−x) −(k/x)e^(−x) −ke^(−x) +k(x+1)(e^(−x) /x) =e^(−x) ln(1+x^2 ) ⇒ k^′ e^(−x) −(k/x)e^(−x) −k e^(−x) +ke^(−x) +(k/x)e^(−x) =e^(−x) ln(1+x^2 ) ⇒ k^′ =ln(1+x^2 ) ⇒k(x) =∫ln(1+x^2 )dx +c but ∫ ln(1+x^2 )dx =_(byparts) xln(1+x^2 )−∫x((2x)/(1+x^2 ))dx =xln(1+x^2 )−2 ∫ ((x^2 +1−1)/(1+x^2 ))dx =xln(1+x^2 )−2+2arctan(x) ⇒ k(x)=xln(1+x^2 )+2arctan(x) +C ⇒ y(x) =(e^(−x) /x)k(x) =(e^(−x) /x)(xln(1+x^2 )+2arctan(x) +C)](Q91052.png)
$$\left({he}\right)\rightarrow{xy}^{'} \:+\left({x}+\mathrm{1}\right){y}\:=\mathrm{0}\:\Rightarrow{xy}^{'} \:=−\left({x}+\mathrm{1}\right){y}\:\Rightarrow\frac{{y}^{'} }{{y}}=−\frac{{x}+\mathrm{1}}{{x}} \\ $$$$=−\mathrm{1}−\frac{\mathrm{1}}{{x}}\:\Rightarrow{ln}\mid{y}\mid\:=−{x}−{ln}\mid{x}\mid\:+{c}\:\Rightarrow{y}\left({x}\right)={k}\:{e}^{−{x}} ×\frac{\mathrm{1}}{\mid{x}\mid} \\ $$$$\left.{solution}\:{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow{y}\left({x}\right)\:={k}\:\frac{{e}^{−{x}} }{{x}}\:\:{let}\:{use}\:{mvc}\:{method}\right. \\ $$$${y}^{'} \:={k}^{'} \:\frac{{e}^{−{x}} }{{x}}\:+{k}\left\{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{e}^{−{x}} \:−\frac{\mathrm{1}}{{x}}{e}^{−{x}} \right\} \\ $$$$\left({e}\right)\Rightarrow{k}^{'} \:{e}^{−{x}} \:−\frac{{k}}{{x}}{e}^{−{x}} −{ke}^{−{x}} \:+{k}\left({x}+\mathrm{1}\right)\frac{{e}^{−{x}} }{{x}}\:={e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${k}^{'} \:{e}^{−{x}} \:−\frac{{k}}{{x}}{e}^{−{x}} \:−{k}\:{e}^{−{x}} \:+{ke}^{−{x}} \:+\frac{{k}}{{x}}{e}^{−{x}} \:={e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${k}^{'} \:={ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\Rightarrow{k}\left({x}\right)\:=\int{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:+{c} \\ $$$${but}\:\int\:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=_{{byparts}} \:\:\:{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\int{x}\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}\:\int\:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}+\mathrm{2}{arctan}\left({x}\right)\:\Rightarrow \\ $$$${k}\left({x}\right)={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\mathrm{2}{arctan}\left({x}\right)\:+{C}\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\frac{{e}^{−{x}} }{{x}}{k}\left({x}\right)\:=\frac{{e}^{−{x}} }{{x}}\left({xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\mathrm{2}{arctan}\left({x}\right)\:+{C}\right) \\ $$
Commented by mathmax by abdo last updated on 27/Apr/20
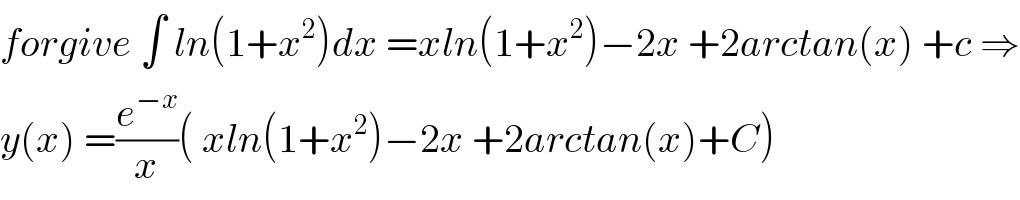
$${forgive}\:\int\:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:={xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}\:+\mathrm{2}{arctan}\left({x}\right)\:+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\frac{{e}^{−{x}} }{{x}}\left(\:{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}\:+\mathrm{2}{arctan}\left({x}\right)+{C}\right) \\ $$
Answered by Joel578 last updated on 27/Apr/20
![y′(x) + p(x)y(x) = r(x) Has the solution y(x) = (1/(F(x)))[∫ F(x)r(x) dx + C] where F(x) is integrating factor and C is integration constant y′ + (1 + (1/x))y = ((e^(−x) ln (1+x^2 ))/x) Integrating factor F(x) = exp[∫ 1 + (1/x) dx] = exp(x + ln x) = xe^x hence y(x) = (e^(−x) /x)[∫ xe^x .((e^(−x) ln (1+x^2 ))/x) dx + C] = (e^(−x) /x)[∫ ln (1+x^2 ) dx + C] Use integration by part: u = ln (1+x^2 ), dv = dx I = x ln (1 + x^2 ) − ∫ ((2x^2 )/(1 + x^2 )) dx = x ln (1 + x^2 ) + ∫ ((2 − 2 − 2x^2 )/(1 + x^2 )) dx = x ln (1 + x^2 ) + ∫ (2/(1 + x^2 )) − 2 dx = x ln (1 + x^2 ) + 2tan^(−1) x − 2x ∴ y(x) = (e^(−x) /x)[x ln (1 + x^2 ) + 2tan^(−1) x − 2x + C]](Q91041.png)
$${y}'\left({x}\right)\:+\:{p}\left({x}\right){y}\left({x}\right)\:=\:{r}\left({x}\right) \\ $$$$\mathrm{Has}\:\mathrm{the}\:\mathrm{solution} \\ $$$${y}\left({x}\right)\:=\:\frac{\mathrm{1}}{{F}\left({x}\right)}\left[\int\:{F}\left({x}\right){r}\left({x}\right)\:{dx}\:+\:{C}\right] \\ $$$$\mathrm{where}\:{F}\left({x}\right)\:\mathrm{is}\:\mathrm{integrating}\:\mathrm{factor}\:\mathrm{and}\:{C}\:\mathrm{is}\:\mathrm{integration}\:\mathrm{constant} \\ $$$$ \\ $$$${y}'\:+\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}}\right){y}\:=\:\frac{{e}^{−{x}} \:\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}} \\ $$$$\mathrm{Integrating}\:\mathrm{factor}\: \\ $$$${F}\left({x}\right)\:=\:\mathrm{exp}\left[\int\:\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}}\:{dx}\right]\:=\:\mathrm{exp}\left({x}\:+\:\mathrm{ln}\:{x}\right)\:=\:{xe}^{{x}} \\ $$$$\mathrm{hence} \\ $$$${y}\left({x}\right)\:=\:\frac{{e}^{−{x}} }{{x}}\left[\int\:{xe}^{{x}} .\frac{{e}^{−{x}} \:\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}}\:{dx}\:+\:{C}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{e}^{−{x}} }{{x}}\left[\int\:\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:{dx}\:+\:{C}\right] \\ $$$$ \\ $$$$\mathrm{Use}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{part}:\:{u}\:=\:\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right),\:{dv}\:=\:{dx}\: \\ $$$${I}\:=\:{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:−\:\int\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:=\:{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:+\:\int\:\frac{\mathrm{2}\:−\:\mathrm{2}\:−\:\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:=\:{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:+\:\int\:\frac{\mathrm{2}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\:−\:\mathrm{2}\:{dx} \\ $$$$\:\:\:=\:{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:+\:\mathrm{2tan}^{−\mathrm{1}} {x}\:−\:\mathrm{2}{x} \\ $$$$ \\ $$$$\therefore\:{y}\left({x}\right)\:=\:\frac{{e}^{−{x}} }{{x}}\left[{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:+\:\mathrm{2tan}^{−\mathrm{1}} {x}\:−\:\mathrm{2}{x}\:+\:{C}\right] \\ $$
Commented by mathmax by abdo last updated on 27/Apr/20

$${thank}\:{you}\:{sir}. \\ $$
