
Previous in Relation and Functions Next in Relation and Functions
Question Number 82476 by abdomathmax last updated on 21/Feb/20
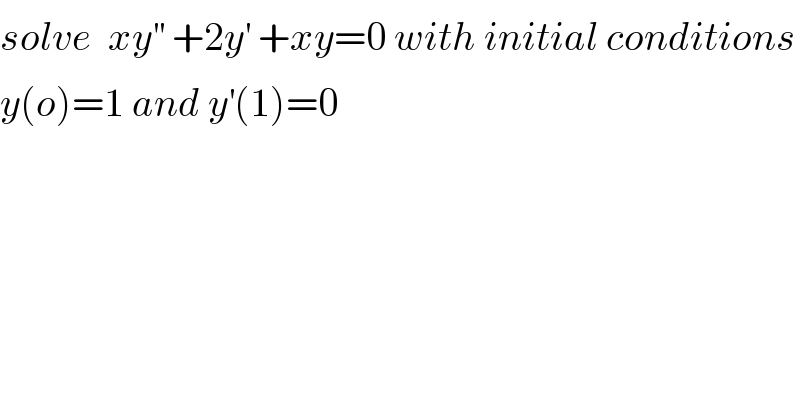
$${solve}\:\:{xy}^{''} \:+\mathrm{2}{y}^{'} \:+{xy}=\mathrm{0}\:{with}\:{initial}\:{conditions} \\ $$$${y}\left({o}\right)=\mathrm{1}\:{and}\:{y}^{'} \left(\mathrm{1}\right)=\mathrm{0} \\ $$
Answered by mind is power last updated on 21/Feb/20

$${z}={xy} \\ $$$$\Rightarrow{z}'={y}+{xy}' \\ $$$${z}''=\mathrm{2}{y}'+{xy}'' \\ $$$${xy}''+\mathrm{2}{y}'+{xy}=\mathrm{0} \\ $$$$\Rightarrow{z}''+{z}=\mathrm{0} \\ $$
