
Question Number 71282 by mr W last updated on 13/Oct/19
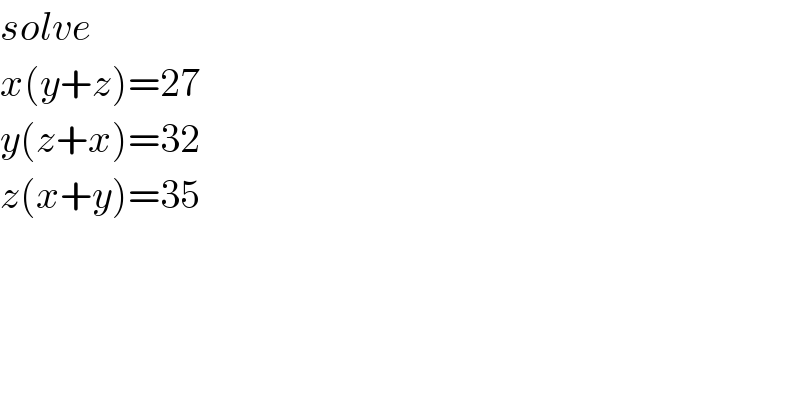
$${solve} \\ $$$${x}\left({y}+{z}\right)=\mathrm{27} \\ $$$${y}\left({z}+{x}\right)=\mathrm{32} \\ $$$${z}\left({x}+{y}\right)=\mathrm{35} \\ $$
Answered by ajfour last updated on 13/Oct/19
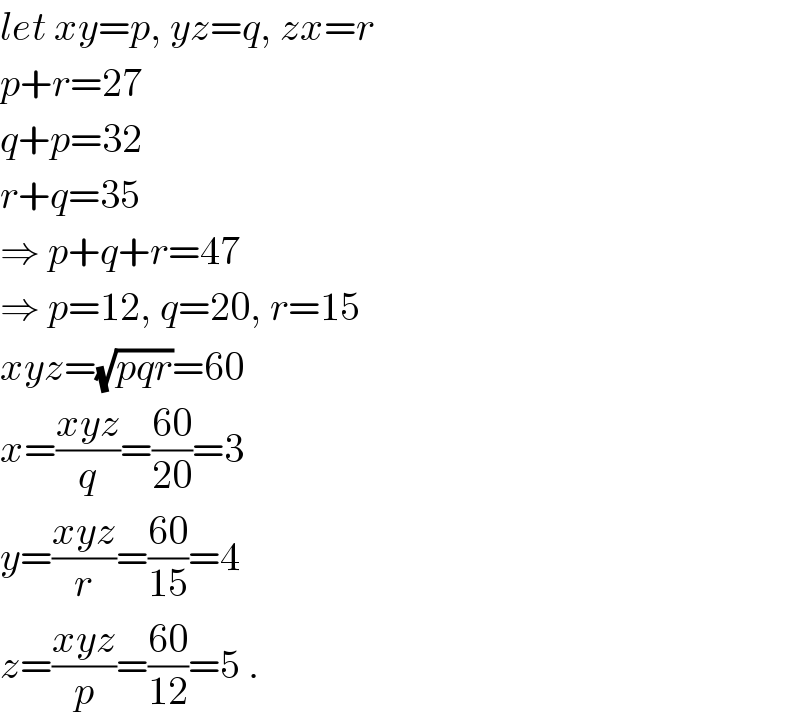
$${let}\:{xy}={p},\:{yz}={q},\:{zx}={r} \\ $$$${p}+{r}=\mathrm{27} \\ $$$${q}+{p}=\mathrm{32} \\ $$$${r}+{q}=\mathrm{35} \\ $$$$\Rightarrow\:{p}+{q}+{r}=\mathrm{47} \\ $$$$\Rightarrow\:{p}=\mathrm{12},\:{q}=\mathrm{20},\:{r}=\mathrm{15} \\ $$$${xyz}=\sqrt{{pqr}}=\mathrm{60} \\ $$$${x}=\frac{{xyz}}{{q}}=\frac{\mathrm{60}}{\mathrm{20}}=\mathrm{3} \\ $$$${y}=\frac{{xyz}}{{r}}=\frac{\mathrm{60}}{\mathrm{15}}=\mathrm{4} \\ $$$${z}=\frac{{xyz}}{{p}}=\frac{\mathrm{60}}{\mathrm{12}}=\mathrm{5}\:. \\ $$
Commented by MJS last updated on 13/Oct/19

$${xyz}=\pm\sqrt{{pqr}} \\ $$
Commented by ajfour last updated on 13/Oct/19
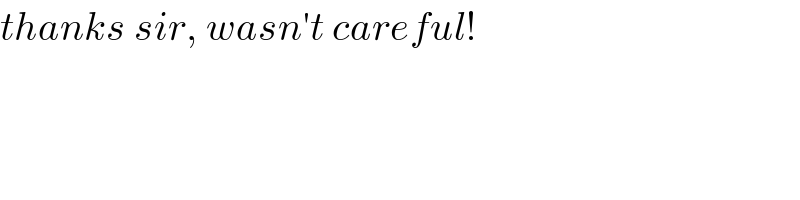
$${thanks}\:{sir},\:{wasn}'{t}\:{careful}! \\ $$
Commented by Rasheed.Sindhi last updated on 13/Oct/19

$$\vee\:\cap{i}\subset\in\:{sir}! \\ $$
Answered by MJS last updated on 13/Oct/19
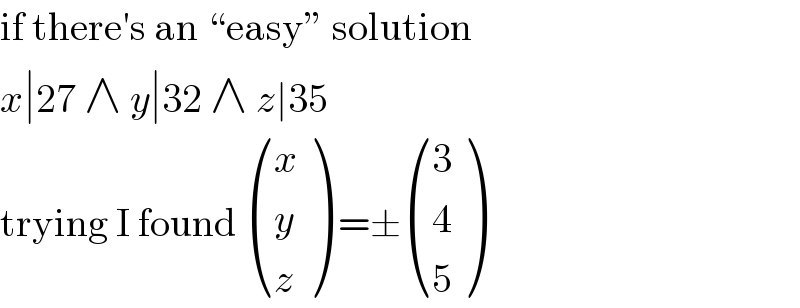
$$\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{an}\:``\mathrm{easy}''\:\mathrm{solution} \\ $$$${x}\mid\mathrm{27}\:\wedge\:{y}\mid\mathrm{32}\:\wedge\:{z}\mid\mathrm{35} \\ $$$$\mathrm{trying}\:\mathrm{I}\:\mathrm{found}\:\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}\:=\pm\begin{pmatrix}{\mathrm{3}}\\{\mathrm{4}}\\{\mathrm{5}}\end{pmatrix} \\ $$
Answered by behi83417@gmail.com last updated on 13/Oct/19
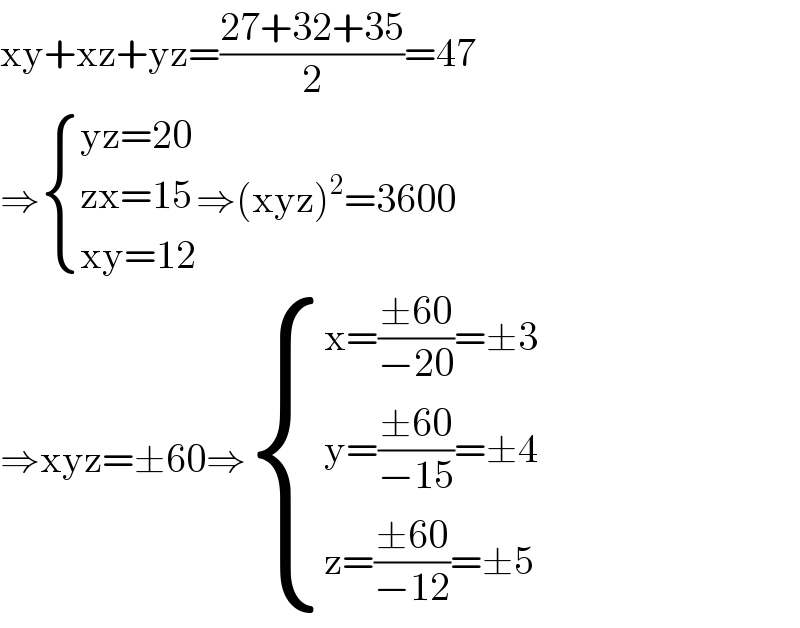
$$\mathrm{xy}+\mathrm{xz}+\mathrm{yz}=\frac{\mathrm{27}+\mathrm{32}+\mathrm{35}}{\mathrm{2}}=\mathrm{47} \\ $$$$\Rightarrow\begin{cases}{\mathrm{yz}=\mathrm{20}}\\{\mathrm{zx}=\mathrm{15}}\\{\mathrm{xy}=\mathrm{12}}\end{cases}\Rightarrow\left(\mathrm{xyz}\right)^{\mathrm{2}} =\mathrm{3600} \\ $$$$\Rightarrow\mathrm{xyz}=\pm\mathrm{60}\Rightarrow\begin{cases}{\mathrm{x}=\frac{\pm\mathrm{60}}{−\mathrm{20}}=\pm\mathrm{3}}\\{\mathrm{y}=\frac{\pm\mathrm{60}}{−\mathrm{15}}=\pm\mathrm{4}}\\{\mathrm{z}=\frac{\pm\mathrm{60}}{−\mathrm{12}}=\pm\mathrm{5}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 13/Oct/19

$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{cellent}}\:\boldsymbol{\mathrm{sir}}! \\ $$
Answered by MJS last updated on 13/Oct/19
![y=p−q∧z=p+q (1) 2px=27 (2) (p−q)(x+p+q)=32 (3) (p+q)(x+p−q)=35 (1) x=((27)/(2p)) (2) 2p^3 −2pq^2 −37p−27q=0 (3) 2p^3 −2pq^2 −43p+27q=0 (2)−(3) 6p−54q=0 ⇒ p=9q (2)=(3) 1440q^3 −360q=0 ⇒ q=±(1/2) [q=0 not valid] ⇒ p=±(9/2) ⇒ x=±3; y=±4; z=±5 ======================== or y=px∧z=qx (1) (p+q)x^2 =27 (2) p(q+1)x^2 =32 (3) (p+1)qx^2 =35 (1) x^2 =((27)/(p+q)) (2) ⇒ 27pq−5p−32q=0 (3) ⇒ 27pa−35p−8q=0 (2)−(3) 30p−24q=0 ⇒ p=(4/5)q (2)=(3) ((108)/5)q^2 −36q=0 ⇒ q=(5/3) [q=0 not valid] ⇒ p=(4/3) ⇒ x^2 =9 ⇒ x=±3; y=±4; z=±5](Q71313.png)
$${y}={p}−{q}\wedge{z}={p}+{q} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{2}{px}=\mathrm{27} \\ $$$$\left(\mathrm{2}\right)\:\:\left({p}−{q}\right)\left({x}+{p}+{q}\right)=\mathrm{32} \\ $$$$\left(\mathrm{3}\right)\:\:\left({p}+{q}\right)\left({x}+{p}−{q}\right)=\mathrm{35} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:{x}=\frac{\mathrm{27}}{\mathrm{2}{p}} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{2}{p}^{\mathrm{3}} −\mathrm{2}{pq}^{\mathrm{2}} −\mathrm{37}{p}−\mathrm{27}{q}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{2}{p}^{\mathrm{3}} −\mathrm{2}{pq}^{\mathrm{2}} −\mathrm{43}{p}+\mathrm{27}{q}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{3}\right)\:\:\mathrm{6}{p}−\mathrm{54}{q}=\mathrm{0}\:\Rightarrow\:{p}=\mathrm{9}{q} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)=\left(\mathrm{3}\right)\:\:\mathrm{1440}{q}^{\mathrm{3}} −\mathrm{360}{q}=\mathrm{0} \\ $$$$\Rightarrow\:{q}=\pm\frac{\mathrm{1}}{\mathrm{2}}\:\:\left[{q}=\mathrm{0}\:\mathrm{not}\:\mathrm{valid}\right] \\ $$$$\Rightarrow\:{p}=\pm\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{3};\:{y}=\pm\mathrm{4};\:{z}=\pm\mathrm{5} \\ $$$$ \\ $$$$======================== \\ $$$$ \\ $$$$\mathrm{or} \\ $$$${y}={px}\wedge{z}={qx} \\ $$$$\left(\mathrm{1}\right)\:\:\left({p}+{q}\right){x}^{\mathrm{2}} =\mathrm{27} \\ $$$$\left(\mathrm{2}\right)\:\:{p}\left({q}+\mathrm{1}\right){x}^{\mathrm{2}} =\mathrm{32} \\ $$$$\left(\mathrm{3}\right)\:\:\left({p}+\mathrm{1}\right){qx}^{\mathrm{2}} =\mathrm{35} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} =\frac{\mathrm{27}}{{p}+{q}} \\ $$$$\left(\mathrm{2}\right)\:\:\Rightarrow\:\mathrm{27}{pq}−\mathrm{5}{p}−\mathrm{32}{q}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\Rightarrow\:\mathrm{27}{pa}−\mathrm{35}{p}−\mathrm{8}{q}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{3}\right)\:\:\mathrm{30}{p}−\mathrm{24}{q}=\mathrm{0}\:\Rightarrow\:{p}=\frac{\mathrm{4}}{\mathrm{5}}{q} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)=\left(\mathrm{3}\right)\:\:\frac{\mathrm{108}}{\mathrm{5}}{q}^{\mathrm{2}} −\mathrm{36}{q}=\mathrm{0} \\ $$$$\Rightarrow\:{q}=\frac{\mathrm{5}}{\mathrm{3}}\:\:\left[{q}=\mathrm{0}\:\mathrm{not}\:\mathrm{valid}\right] \\ $$$$\Rightarrow\:{p}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{3};\:{y}=\pm\mathrm{4};\:{z}=\pm\mathrm{5} \\ $$
