
Question Number 71824 by mr W last updated on 20/Oct/19
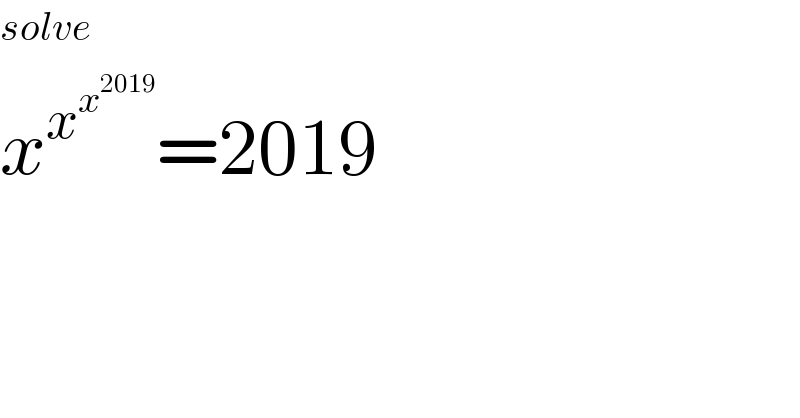
$${solve}\: \\ $$$${x}^{{x}^{{x}^{\mathrm{2019}} } } =\mathrm{2019} \\ $$
Commented by mr W last updated on 21/Oct/19

$${we}\:{can}\:{see}: \\ $$$${if}\:{we}\:{assume}\:{x}^{\mathrm{2019}} =\mathrm{2019},\:{we}\:{will}\:{get} \\ $$$${x}^{{x}^{\mathrm{2019}} } ={x}^{\mathrm{2019}} =\mathrm{2019} \\ $$$${x}^{{x}^{{x}^{\mathrm{2019}} } } ={x}^{\mathrm{2019}} =\mathrm{2019} \\ $$$${x}^{{x}^{{x}^{{x}^{\mathrm{2019}} } } } ={x}^{\mathrm{2019}} =\mathrm{2019} \\ $$$$.... \\ $$$${i}.{e}.\:{the}\:{assumption}\:{x}^{\mathrm{2019}} =\mathrm{2019}\:{is}\:{correct}. \\ $$$${from}\:{x}^{\mathrm{2019}} =\mathrm{2019},\:{we}\:{get} \\ $$$$\Rightarrow\:{x}=\sqrt[{\mathrm{2019}}]{\mathrm{2019}} \\ $$
Answered by MJS last updated on 20/Oct/19

$$\mathrm{usually}\:{x}^{{x}^{{x}^{\mathrm{2019}} } } ={x}^{\left({x}^{\left({x}^{\mathrm{2019}} \right)} \right)} \\ $$$${x}^{\left({x}^{\left({x}^{\mathrm{2019}} \right)} \right)} =\mathrm{2019}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{1}.\mathrm{00377648280}<{x}<\mathrm{1}.\mathrm{00377648281} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\left(\left({x}^{{x}} \right)^{{x}} \right)^{\mathrm{2019}} =\mathrm{2019}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{1}.\mathrm{00374827787}<{x}<\mathrm{1}.\mathrm{00374827788} \\ $$
Commented by mr W last updated on 21/Oct/19
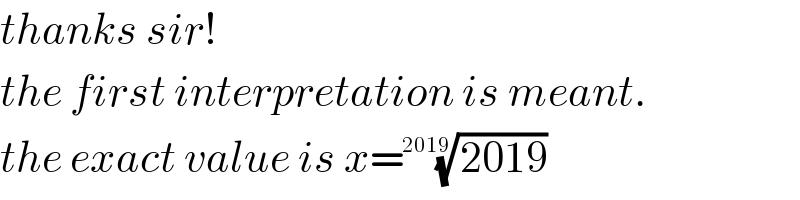
$${thanks}\:{sir}! \\ $$$${the}\:{first}\:{interpretation}\:{is}\:{meant}. \\ $$$${the}\:{exact}\:{value}\:{is}\:{x}=\sqrt[{\mathrm{2019}}]{\mathrm{2019}} \\ $$
Commented by TawaTawa last updated on 21/Oct/19
$$\mathrm{Please}\:\mathrm{workings}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 22/Oct/19

$${see}\:{above}. \\ $$$${the}\:{result}\:{is}\:{the}\:{same},\:{no}\:{matter}\: \\ $$$${how}\:{many}\:{times}\:{x}\:{occurs}\:{in}\:{the} \\ $$$${equation}. \\ $$
Answered by mind is power last updated on 23/Oct/19
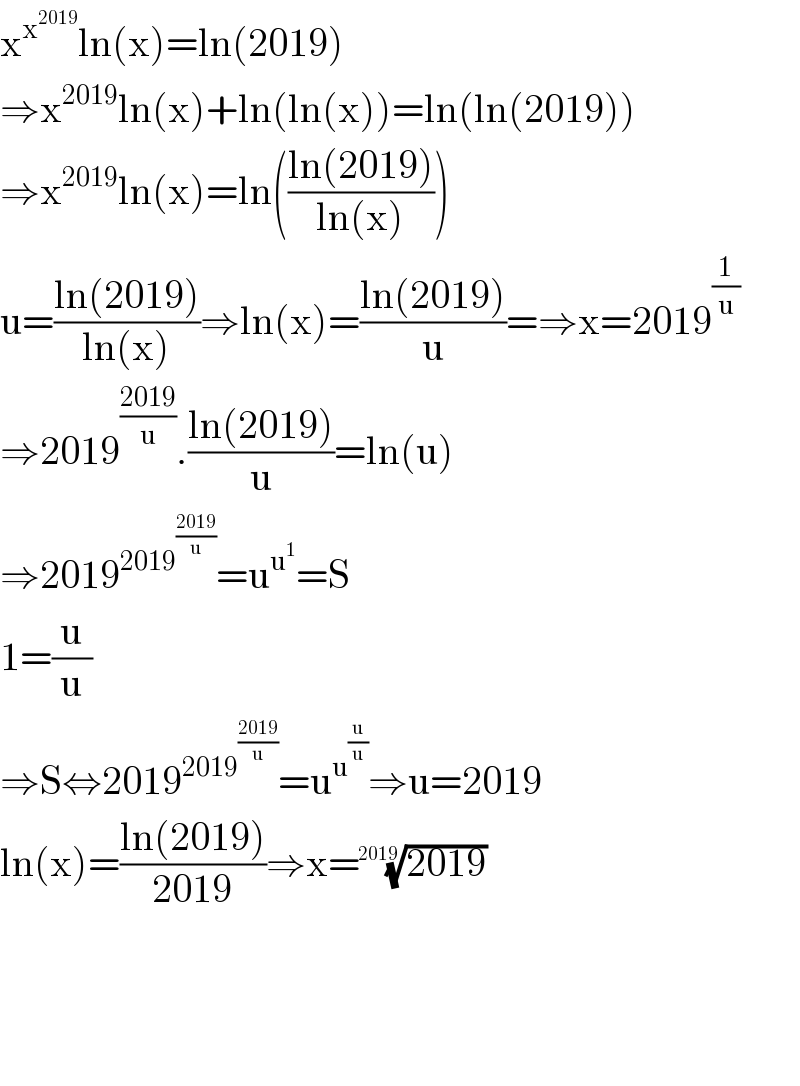
$$\mathrm{x}^{\mathrm{x}^{\mathrm{2019}} } \mathrm{ln}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{2019}\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2019}} \mathrm{ln}\left(\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{x}\right)\right)=\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{2019}\right)\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2019}} \mathrm{ln}\left(\mathrm{x}\right)=\mathrm{ln}\left(\frac{\mathrm{ln}\left(\mathrm{2019}\right)}{\mathrm{ln}\left(\mathrm{x}\right)}\right) \\ $$$$\mathrm{u}=\frac{\mathrm{ln}\left(\mathrm{2019}\right)}{\mathrm{ln}\left(\mathrm{x}\right)}\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{2019}\right)}{\mathrm{u}}=\Rightarrow\mathrm{x}=\mathrm{2019}^{\frac{\mathrm{1}}{\mathrm{u}}} \\ $$$$\Rightarrow\mathrm{2019}^{\frac{\mathrm{2019}}{\mathrm{u}}} .\frac{\mathrm{ln}\left(\mathrm{2019}\right)}{\mathrm{u}}=\mathrm{ln}\left(\mathrm{u}\right) \\ $$$$\Rightarrow\mathrm{2019}^{\mathrm{2019}^{\frac{\mathrm{2019}}{\mathrm{u}}} } =\mathrm{u}^{\mathrm{u}^{\mathrm{1}} } =\mathrm{S} \\ $$$$\mathrm{1}=\frac{\mathrm{u}}{\mathrm{u}} \\ $$$$\Rightarrow\mathrm{S}\Leftrightarrow\mathrm{2019}^{\mathrm{2019}^{\frac{\mathrm{2019}}{\mathrm{u}}} } =\mathrm{u}^{\mathrm{u}^{\frac{\mathrm{u}}{\mathrm{u}}} } \Rightarrow\mathrm{u}=\mathrm{2019} \\ $$$$\mathrm{ln}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{2019}\right)}{\mathrm{2019}}\Rightarrow\mathrm{x}=\sqrt[{\mathrm{2019}}]{\mathrm{2019}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 23/Oct/19

$${thanks}\:{alot}\:{sir}! \\ $$
Commented by mind is power last updated on 23/Oct/19

$$\mathrm{y}\:'\mathrm{re}\:\mathrm{welcom}\:\: \\ $$
