
Question Number 109193 by mr W last updated on 21/Aug/20

$${solve}\: \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{5} \\ $$
Commented by aurpeyz last updated on 21/Aug/20

$$\:{x}^{{x}^{\mathrm{3}} } =\mathrm{2}^{\mathrm{2}} \\ $$$${x}^{\mathrm{3}} =\mathrm{2} \\ $$$${x}\underset{} {=}^{\mathrm{3}} \sqrt{\mathrm{2}} \\ $$
Commented by aurpeyz last updated on 21/Aug/20
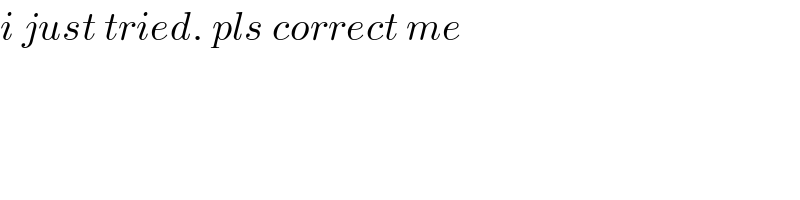
$${i}\:{just}\:{tried}.\:{pls}\:{correct}\:{me} \\ $$
Commented by mr W last updated on 21/Aug/20
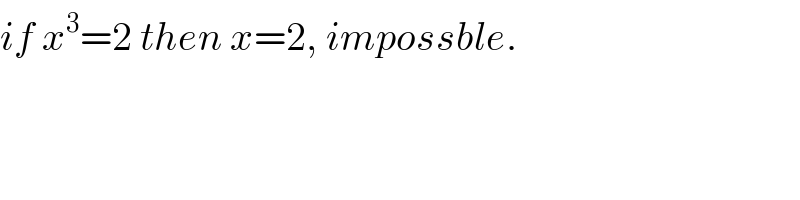
$${if}\:{x}^{\mathrm{3}} =\mathrm{2}\:{then}\:{x}=\mathrm{2},\:{impossble}. \\ $$
Commented by mr W last updated on 21/Aug/20
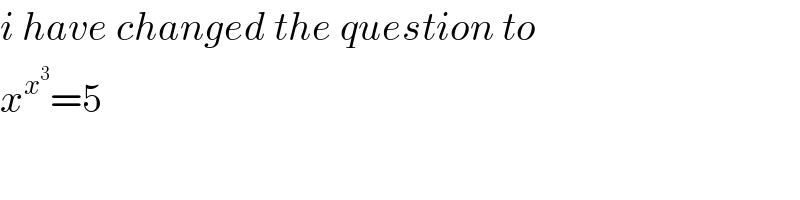
$${i}\:{have}\:{changed}\:{the}\:{question}\:{to} \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{5} \\ $$
Commented by aurpeyz last updated on 21/Aug/20
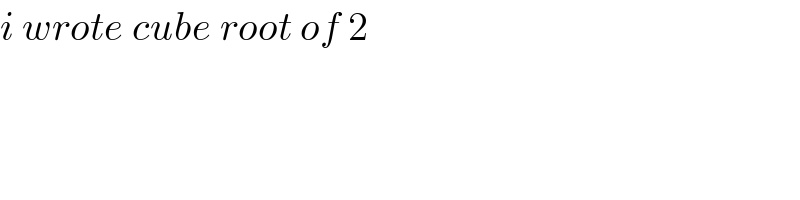
$${i}\:{wrote}\:{cube}\:{root}\:{of}\:\mathrm{2} \\ $$
Commented by aurpeyz last updated on 21/Aug/20
$${okay}\:{sir}.\:{i}\:{will}\:{try} \\ $$
Commented by mr W last updated on 21/Aug/20
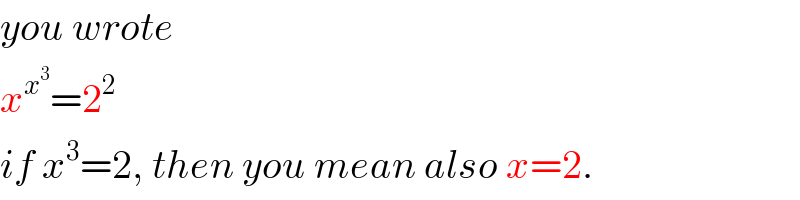
$${you}\:{wrote} \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{2}^{\mathrm{2}} \\ $$$${if}\:{x}^{\mathrm{3}} =\mathrm{2},\:{then}\:{you}\:{mean}\:{also}\:{x}=\mathrm{2}. \\ $$
Commented by aurpeyz last updated on 21/Aug/20
$${yes}.\:{i}\:{am}\:{wrong}.\:{if}\:{the}\:{indeces}\:{are}\:{equal}.\:{the}\:{base} \\ $$$${will}\:{be}\:{equal}. \\ $$
Answered by Dwaipayan Shikari last updated on 21/Aug/20

$${x}^{\mathrm{3}} {logx}={log}\mathrm{5} \\ $$$$\mathrm{3}{logx}\:{e}^{\mathrm{3}{logx}} =\mathrm{3}{log}\mathrm{5} \\ $$$$\mathrm{3}{logx}={W}_{\mathrm{0}} \left(\mathrm{3}{log}\mathrm{5}\right) \\ $$$${x}={e}^{\frac{{W}_{\mathrm{0}} \left(\mathrm{3}{log}\mathrm{5}\right)}{\mathrm{3}}} =\mathrm{1}.\mathrm{5459}.. \\ $$
Commented by mr W last updated on 21/Aug/20

$${good}! \\ $$
Answered by Aziztisffola last updated on 21/Aug/20
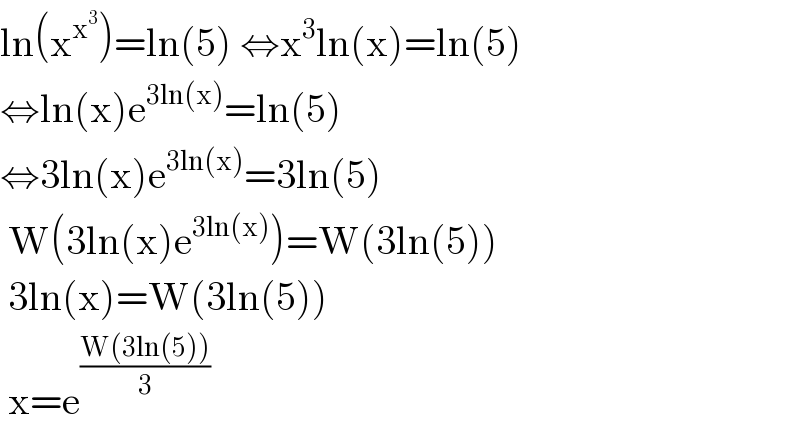
$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{x}^{\mathrm{3}} } \right)=\mathrm{ln}\left(\mathrm{5}\right)\:\Leftrightarrow\mathrm{x}^{\mathrm{3}} \mathrm{ln}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{5}\right) \\ $$$$\Leftrightarrow\mathrm{ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} =\mathrm{ln}\left(\mathrm{5}\right) \\ $$$$\Leftrightarrow\mathrm{3ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} =\mathrm{3ln}\left(\mathrm{5}\right) \\ $$$$\:\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} \right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right) \\ $$$$\:\mathrm{3ln}\left(\mathrm{x}\right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right) \\ $$$$\:\mathrm{x}=\mathrm{e}^{\frac{\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right)}{\mathrm{3}}} \\ $$
Commented by aurpeyz last updated on 24/Aug/20
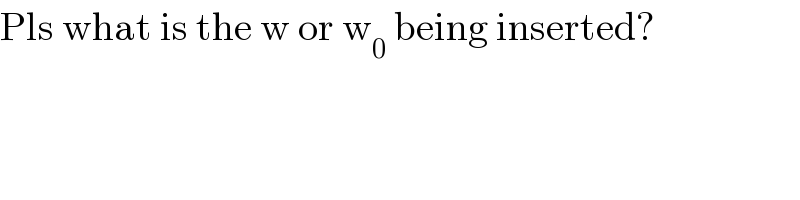
$$\mathrm{Pls}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{w}\:\mathrm{or}\:\mathrm{w}_{\mathrm{0}} \:\mathrm{being}\:\mathrm{inserted}? \\ $$
Commented by Aziztisffola last updated on 24/Aug/20
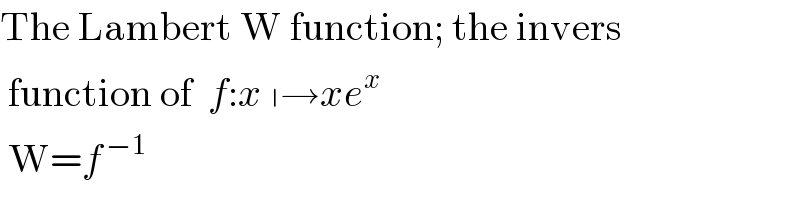
$$\mathrm{The}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{function};\:\mathrm{the}\:\mathrm{invers}\: \\ $$$$\:\mathrm{function}\:\mathrm{of}\:\:{f}:{x}\:\shortmid\rightarrow{xe}^{{x}} \\ $$$$\:\mathrm{W}={f}^{\:−\mathrm{1}\:} \\ $$
Commented by aurpeyz last updated on 25/Aug/20
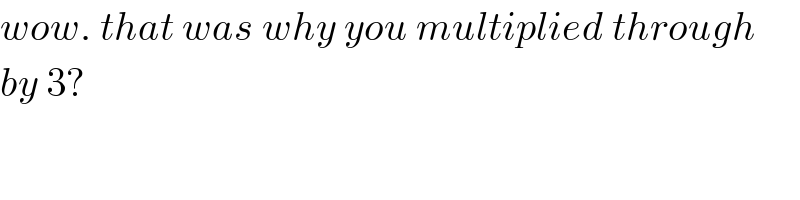
$${wow}.\:{that}\:{was}\:{why}\:{you}\:{multiplied}\:{through} \\ $$$${by}\:\mathrm{3}? \\ $$
Answered by 1549442205PVT last updated on 22/Aug/20
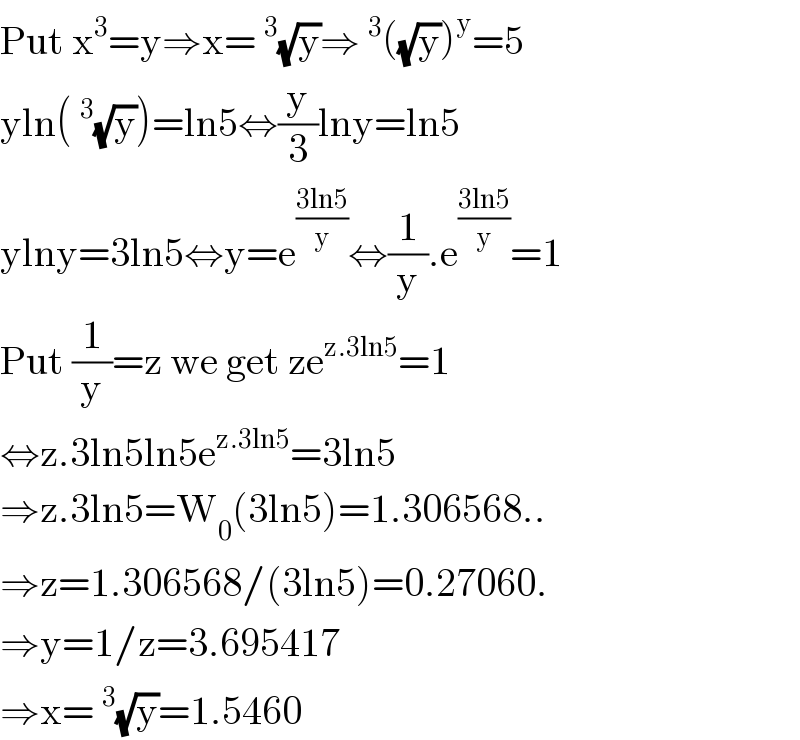
$$\mathrm{Put}\:\mathrm{x}^{\mathrm{3}} =\mathrm{y}\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{y}}\Rightarrow\:^{\mathrm{3}} \left(\sqrt{\mathrm{y}}\right)^{\mathrm{y}} =\mathrm{5} \\ $$$$\mathrm{yln}\left(\:^{\mathrm{3}} \sqrt{\mathrm{y}}\right)=\mathrm{ln5}\Leftrightarrow\frac{\mathrm{y}}{\mathrm{3}}\mathrm{lny}=\mathrm{ln5} \\ $$$$\mathrm{ylny}=\mathrm{3ln5}\Leftrightarrow\mathrm{y}=\mathrm{e}^{\frac{\mathrm{3ln5}}{\mathrm{y}}} \Leftrightarrow\frac{\mathrm{1}}{\mathrm{y}}.\mathrm{e}^{\frac{\mathrm{3ln5}}{\mathrm{y}}} =\mathrm{1} \\ $$$$\mathrm{Put}\:\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{z}\:\mathrm{we}\:\mathrm{get}\:\mathrm{ze}^{\mathrm{z}.\mathrm{3ln5}} =\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{z}.\mathrm{3ln5ln5e}^{\mathrm{z}.\mathrm{3ln5}} =\mathrm{3ln5} \\ $$$$\Rightarrow\mathrm{z}.\mathrm{3ln5}=\mathrm{W}_{\mathrm{0}} \left(\mathrm{3ln5}\right)=\mathrm{1}.\mathrm{306568}.. \\ $$$$\Rightarrow\mathrm{z}=\mathrm{1}.\mathrm{306568}/\left(\mathrm{3ln5}\right)=\mathrm{0}.\mathrm{27060}. \\ $$$$\Rightarrow\mathrm{y}=\mathrm{1}/\mathrm{z}=\mathrm{3}.\mathrm{695417} \\ $$$$\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{y}}=\mathrm{1}.\mathrm{5460} \\ $$
