
Question Number 171871 by Mikenice last updated on 21/Jun/22
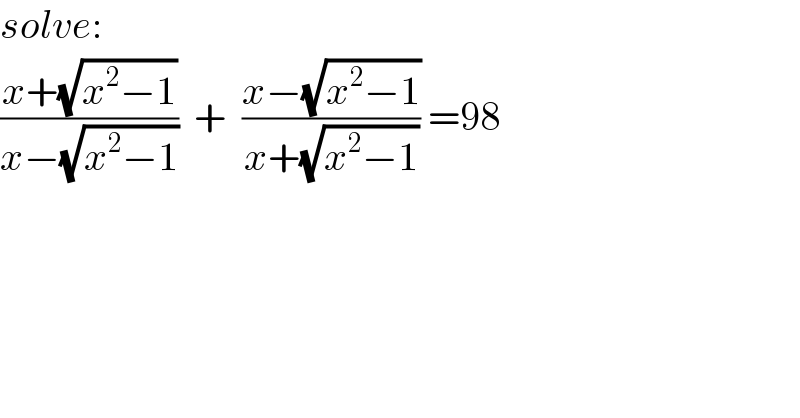
$${solve}: \\ $$$$\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\:+\:\:\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{98} \\ $$
Commented by infinityaction last updated on 21/Jun/22

$$\pm\mathrm{5} \\ $$
Commented by Mikenice last updated on 21/Jun/22

$${please}\:{sir}\:{show}\:{the}\:{solution} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 21/Jun/22
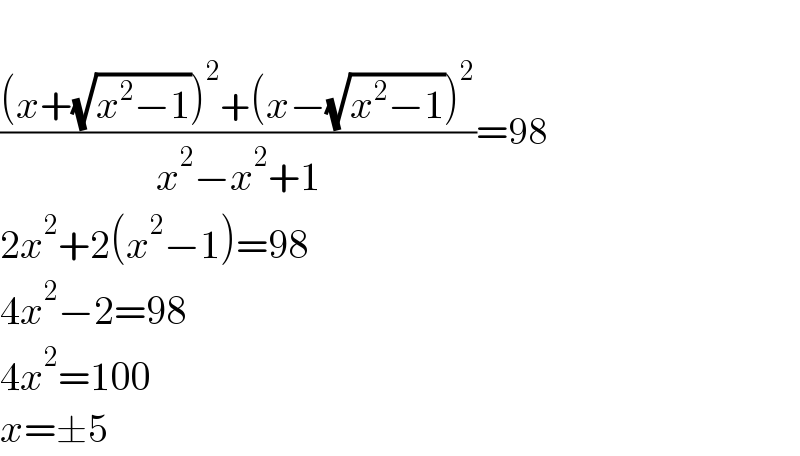
$$ \\ $$$$\frac{\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} +\left({x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{98} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{98} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{98} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} =\mathrm{100} \\ $$$${x}=\pm\mathrm{5} \\ $$
Commented by Mikenice last updated on 23/Jun/22

$${thanks}\:{sir} \\ $$
