
Question Number 105080 by 175mohamed last updated on 25/Jul/20
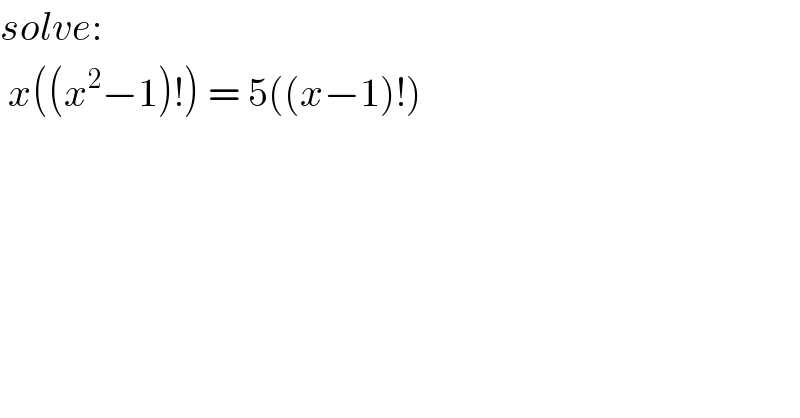
$${solve}: \\ $$$$\:{x}\left(\left({x}^{\mathrm{2}} −\mathrm{1}\right)!\right)\:=\:\mathrm{5}\left(\left({x}−\mathrm{1}\right)!\right) \\ $$
Answered by JDamian last updated on 25/Jul/20
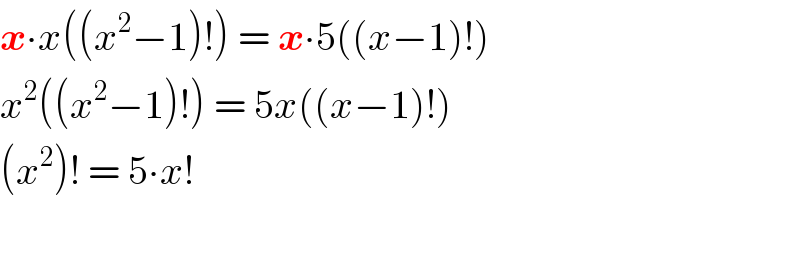
$$\boldsymbol{{x}}\centerdot{x}\left(\left({x}^{\mathrm{2}} −\mathrm{1}\right)!\right)\:=\:\boldsymbol{{x}}\centerdot\mathrm{5}\left(\left({x}−\mathrm{1}\right)!\right) \\ $$$${x}^{\mathrm{2}} \left(\left({x}^{\mathrm{2}} −\mathrm{1}\right)!\right)\:=\:\mathrm{5}{x}\left(\left({x}−\mathrm{1}\right)!\right) \\ $$$$\left({x}^{\mathrm{2}} \right)!\:=\:\mathrm{5}\centerdot{x}! \\ $$$$ \\ $$
Answered by OlafThorendsen last updated on 25/Jul/20
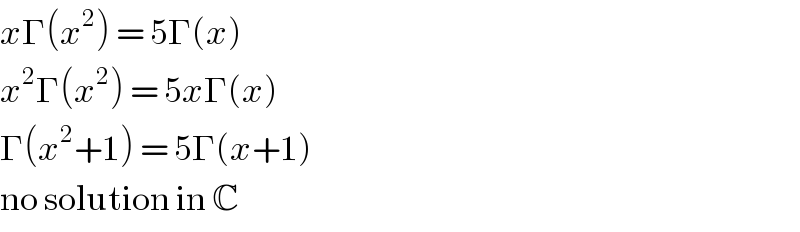
$${x}\Gamma\left({x}^{\mathrm{2}} \right)\:=\:\mathrm{5}\Gamma\left({x}\right) \\ $$$${x}^{\mathrm{2}} \Gamma\left({x}^{\mathrm{2}} \right)\:=\:\mathrm{5}{x}\Gamma\left({x}\right) \\ $$$$\Gamma\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{5}\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{C} \\ $$
