
Question Number 209341 by Tawa11 last updated on 07/Jul/24
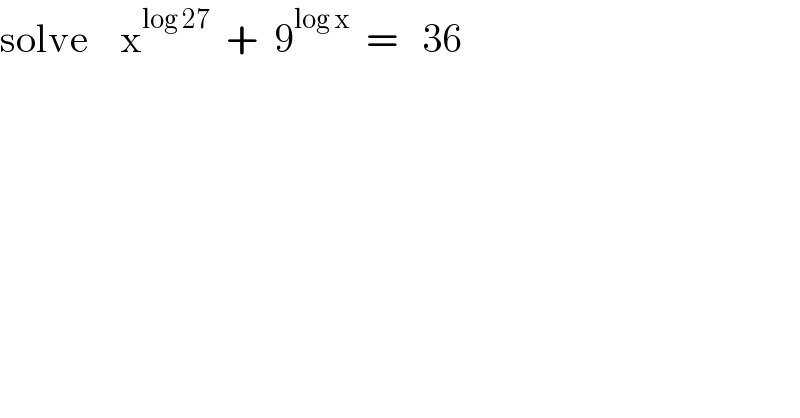
$$\mathrm{solve}\:\:\:\:\mathrm{x}^{\mathrm{log}\:\mathrm{27}} \:\:+\:\:\mathrm{9}^{\mathrm{log}\:\mathrm{x}} \:\:=\:\:\:\mathrm{36} \\ $$
Answered by Frix last updated on 07/Jul/24
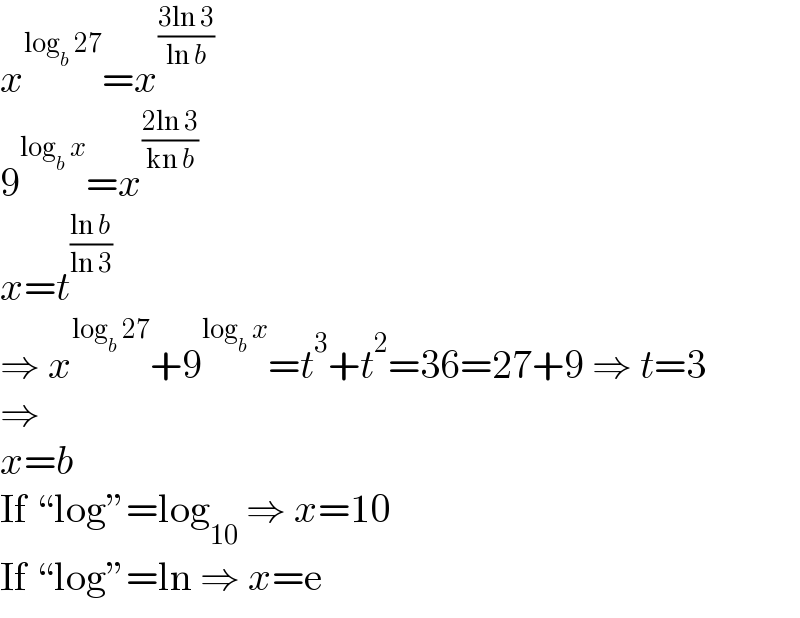
$${x}^{\mathrm{log}_{{b}} \:\mathrm{27}} ={x}^{\frac{\mathrm{3ln}\:\mathrm{3}}{\mathrm{ln}\:{b}}} \\ $$$$\mathrm{9}^{\mathrm{log}_{{b}} \:{x}} ={x}^{\frac{\mathrm{2ln}\:\mathrm{3}}{\mathrm{kn}\:{b}}} \\ $$$${x}={t}^{\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:\mathrm{3}}} \\ $$$$\Rightarrow\:{x}^{\mathrm{log}_{{b}} \:\mathrm{27}} +\mathrm{9}^{\mathrm{log}_{{b}} \:{x}} ={t}^{\mathrm{3}} +{t}^{\mathrm{2}} =\mathrm{36}=\mathrm{27}+\mathrm{9}\:\Rightarrow\:{t}=\mathrm{3} \\ $$$$\Rightarrow \\ $$$${x}={b} \\ $$$$\mathrm{If}\:``\mathrm{log}''=\mathrm{log}_{\mathrm{10}} \:\Rightarrow\:{x}=\mathrm{10} \\ $$$$\mathrm{If}\:``\mathrm{log}''=\mathrm{ln}\:\Rightarrow\:{x}=\mathrm{e} \\ $$
Commented by Tawa11 last updated on 07/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by Kademi last updated on 09/Jul/24
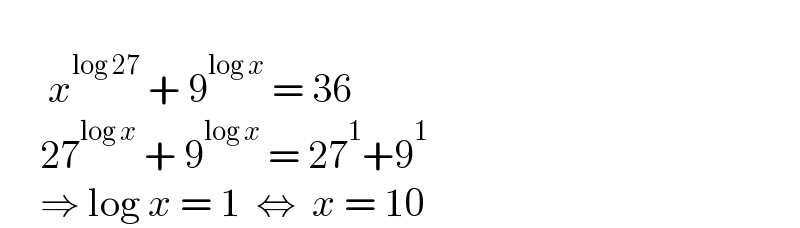
$$\: \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{log}\:\mathrm{27}} \:+\:\mathrm{9}^{\mathrm{log}\:{x}} \:=\:\mathrm{36} \\ $$$$\:\:\:\:\:\mathrm{27}^{\mathrm{log}\:{x}} \:+\:\mathrm{9}^{\mathrm{log}\:{x}} \:=\:\mathrm{27}^{\mathrm{1}} +\mathrm{9}^{\mathrm{1}} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{log}\:{x}\:=\:\mathrm{1}\:\:\Leftrightarrow\:\:{x}\:=\:\mathrm{10} \\ $$
Commented by Tawa11 last updated on 09/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
