
Question Number 5902 by Ashis last updated on 04/Jun/16
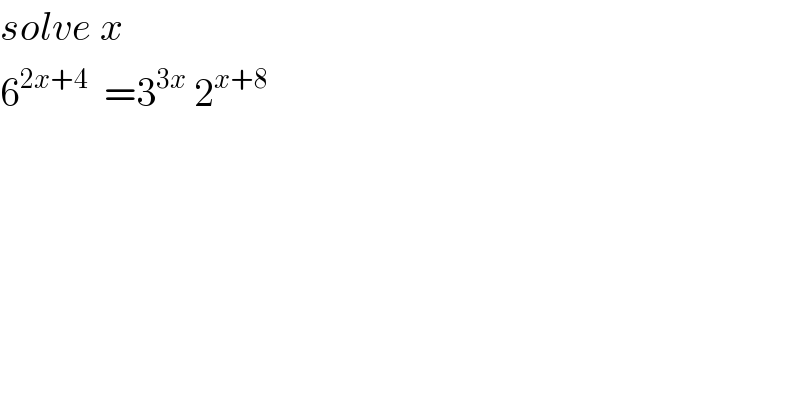
$${solve}\:{x} \\ $$$$\mathrm{6}^{\mathrm{2}{x}+\mathrm{4}} \:\:=\mathrm{3}^{\mathrm{3}{x}} \:\mathrm{2}^{{x}+\mathrm{8}} \\ $$
Commented by prakash jain last updated on 04/Jun/16
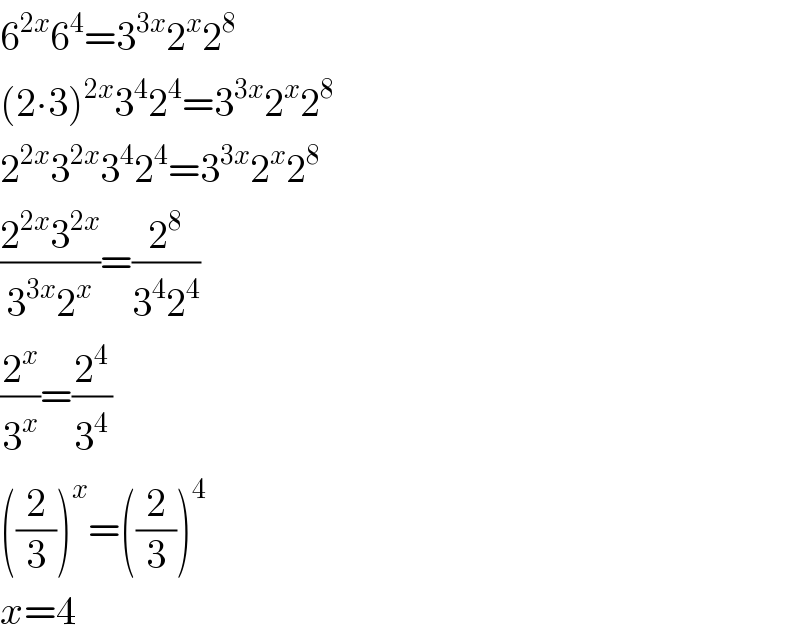
$$\mathrm{6}^{\mathrm{2}{x}} \mathrm{6}^{\mathrm{4}} =\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}} \mathrm{2}^{\mathrm{8}} \\ $$$$\left(\mathrm{2}\centerdot\mathrm{3}\right)^{\mathrm{2}{x}} \mathrm{3}^{\mathrm{4}} \mathrm{2}^{\mathrm{4}} =\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}} \mathrm{2}^{\mathrm{8}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} \mathrm{3}^{\mathrm{2}{x}} \mathrm{3}^{\mathrm{4}} \mathrm{2}^{\mathrm{4}} =\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}} \mathrm{2}^{\mathrm{8}} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}{x}} \mathrm{3}^{\mathrm{2}{x}} }{\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}} }=\frac{\mathrm{2}^{\mathrm{8}} }{\mathrm{3}^{\mathrm{4}} \mathrm{2}^{\mathrm{4}} } \\ $$$$\frac{\mathrm{2}^{{x}} }{\mathrm{3}^{{x}} }=\frac{\mathrm{2}^{\mathrm{4}} }{\mathrm{3}^{\mathrm{4}} } \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{4}} \\ $$$${x}=\mathrm{4} \\ $$
Answered by sanusihammed last updated on 04/Jun/16

$${Solution} \\ $$$$ \\ $$$$\mathrm{6}^{\mathrm{2}{x}\:+\:\mathrm{4}} \:=\:\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}+\mathrm{8}} \\ $$$${Take}\:{the}\:{logarithm}\:{of}\:{both}\:{sides} \\ $$$${log}\mathrm{6}^{\mathrm{2}{x}+\mathrm{4}} \:=\:{log}\left(\mathrm{3}^{\mathrm{3}{x}} \mathrm{2}^{{x}+\mathrm{8}} \right) \\ $$$$\left(\mathrm{2}{x}+\mathrm{4}\right){log}\mathrm{6}\:=\:{log}\mathrm{3}^{\mathrm{3}{x}} \:+\:{log}\mathrm{2}^{{x}+\mathrm{8}} \\ $$$$\left(\mathrm{2}{x}+\mathrm{4}\right){log}\mathrm{6}\:=\:\mathrm{3}{xlog}\mathrm{3}\:+\:\left({x}+\mathrm{8}\right){log}\mathrm{2} \\ $$$$\left(\mathrm{2}{x}+\mathrm{4}\right)\mathrm{0}.\mathrm{7782}\:=\:\mathrm{3}{x}\left(\mathrm{0}.\mathrm{4771}\right)\:+\:\left({x}+\mathrm{8}\right)\left(\mathrm{0}.\mathrm{3010}\right) \\ $$$$\mathrm{1}.\mathrm{5564}{x}\:+\:\mathrm{3}.\mathrm{1128}\:=\:\mathrm{1}.\mathrm{4313}{x}\:+\:\mathrm{0}.\mathrm{3010}{x}\:+\:\mathrm{2}.\mathrm{408} \\ $$$$\mathrm{1}.\mathrm{5564}{x}\:+\:\mathrm{3}.\mathrm{1128}\:=\:\mathrm{1}.\mathrm{7323}{x}\:+\:\mathrm{2}.\mathrm{408} \\ $$$${collect}\:{the}\:{like}\:{terms} \\ $$$$\mathrm{1}.\mathrm{7323}{x}−\mathrm{1}.\mathrm{5564}{x}\:=\:\mathrm{3}.\mathrm{1128}−\mathrm{2}.\mathrm{408} \\ $$$$\mathrm{0}.\mathrm{1759}{x}\:=\:\mathrm{0}.\mathrm{7048} \\ $$$${x}\:=\:\frac{\mathrm{0}.\mathrm{7048}}{\mathrm{0}.\mathrm{1759}} \\ $$$${x}\:=\:\mathrm{4}.\mathrm{0068} \\ $$$${Approximately} \\ $$$${x}\:=\:\mathrm{4} \\ $$$$ \\ $$$$ \\ $$
