
Question Number 117027 by I want to learn more last updated on 09/Oct/20
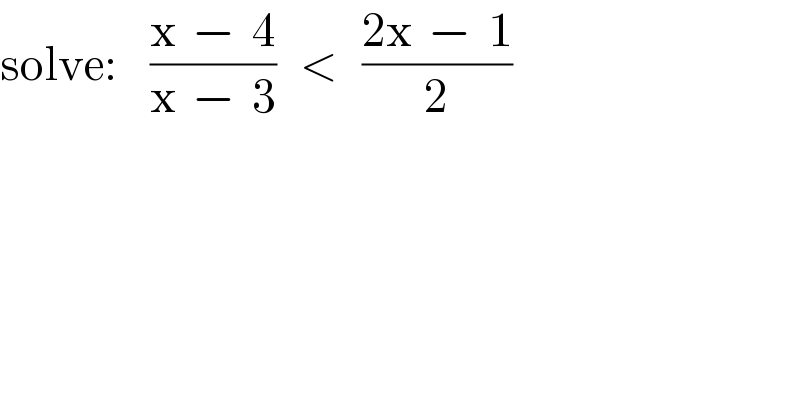
$$\mathrm{solve}:\:\:\:\:\frac{\mathrm{x}\:\:−\:\:\mathrm{4}}{\mathrm{x}\:\:−\:\:\mathrm{3}}\:\:\:<\:\:\:\frac{\mathrm{2x}\:\:−\:\:\mathrm{1}}{\mathrm{2}} \\ $$
Answered by bemath last updated on 09/Oct/20
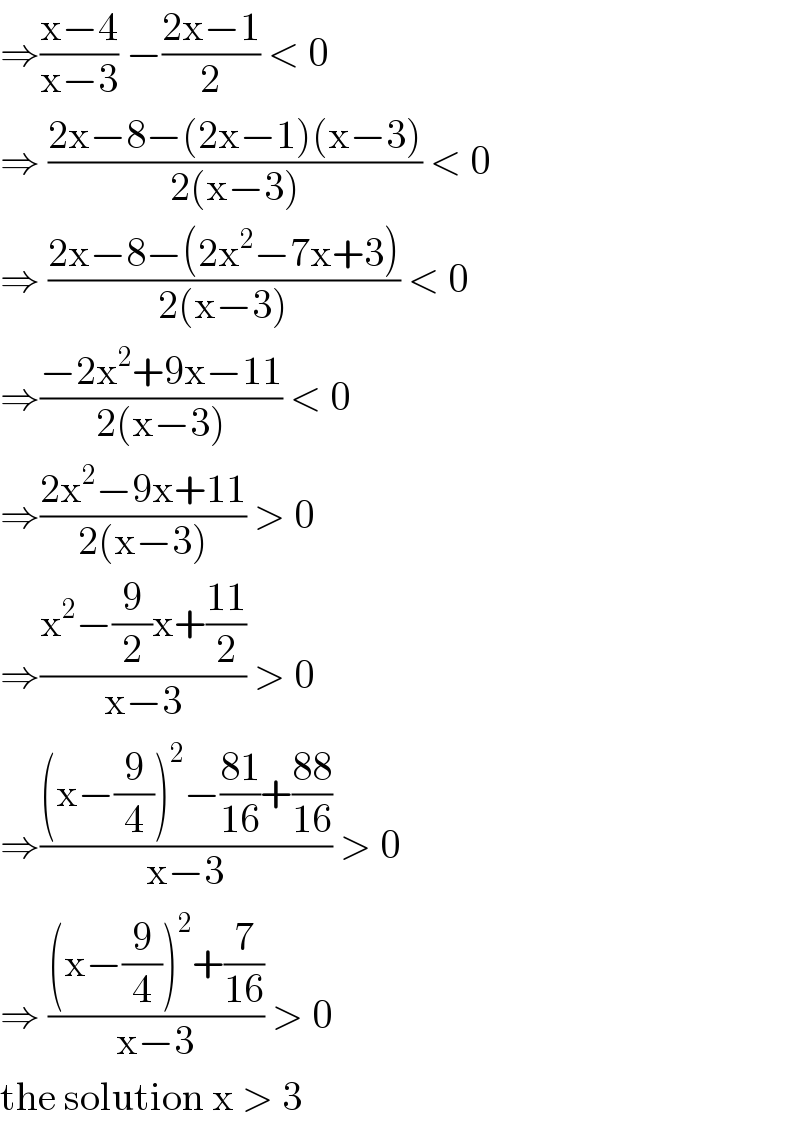
$$\Rightarrow\frac{\mathrm{x}−\mathrm{4}}{\mathrm{x}−\mathrm{3}}\:−\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2}}\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{2x}−\mathrm{8}−\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)}\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{2x}−\mathrm{8}−\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{7x}+\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)}\:<\:\mathrm{0} \\ $$$$\Rightarrow\frac{−\mathrm{2x}^{\mathrm{2}} +\mathrm{9x}−\mathrm{11}}{\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)}\:<\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{9x}+\mathrm{11}}{\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)}\:>\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}+\frac{\mathrm{11}}{\mathrm{2}}}{\mathrm{x}−\mathrm{3}}\:>\:\mathrm{0} \\ $$$$\Rightarrow\frac{\left(\mathrm{x}−\frac{\mathrm{9}}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{81}}{\mathrm{16}}+\frac{\mathrm{88}}{\mathrm{16}}}{\mathrm{x}−\mathrm{3}}\:>\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{x}−\frac{\mathrm{9}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{16}}}{\mathrm{x}−\mathrm{3}}\:>\:\mathrm{0}\: \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{x}\:>\:\mathrm{3} \\ $$
Commented by I want to learn more last updated on 09/Oct/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by 1549442205PVT last updated on 09/Oct/20
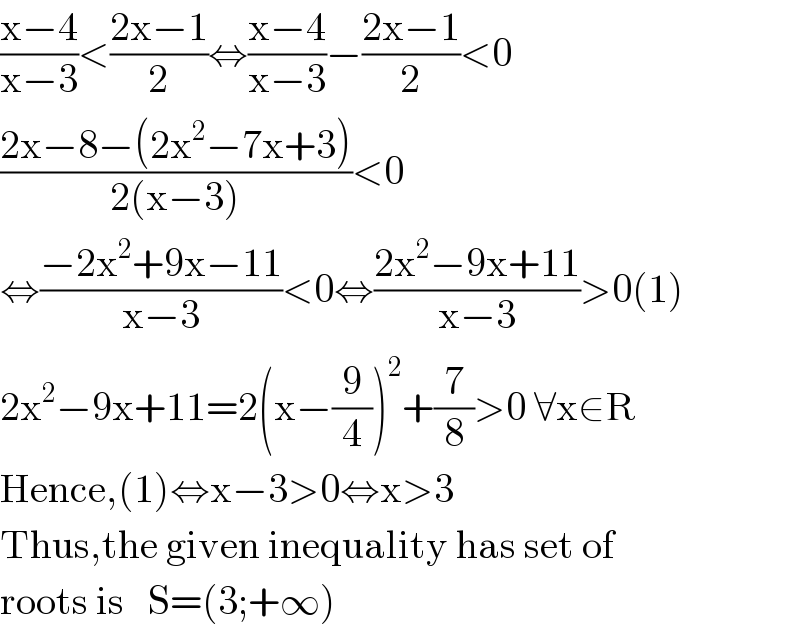
$$\frac{\mathrm{x}−\mathrm{4}}{\mathrm{x}−\mathrm{3}}<\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2}}\Leftrightarrow\frac{\mathrm{x}−\mathrm{4}}{\mathrm{x}−\mathrm{3}}−\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2}}<\mathrm{0} \\ $$$$\frac{\mathrm{2x}−\mathrm{8}−\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{7x}+\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)}<\mathrm{0} \\ $$$$\Leftrightarrow\frac{−\mathrm{2x}^{\mathrm{2}} +\mathrm{9x}−\mathrm{11}}{\mathrm{x}−\mathrm{3}}<\mathrm{0}\Leftrightarrow\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{9x}+\mathrm{11}}{\mathrm{x}−\mathrm{3}}>\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{9x}+\mathrm{11}=\mathrm{2}\left(\mathrm{x}−\frac{\mathrm{9}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{8}}>\mathrm{0}\:\forall\mathrm{x}\in\mathrm{R} \\ $$$$\mathrm{Hence},\left(\mathrm{1}\right)\Leftrightarrow\mathrm{x}−\mathrm{3}>\mathrm{0}\Leftrightarrow\mathrm{x}>\mathrm{3} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{has}\:\mathrm{set}\:\mathrm{of} \\ $$$$\mathrm{roots}\:\mathrm{is}\:\:\:\mathrm{S}=\left(\mathrm{3};+\infty\right) \\ $$
Commented by bemath last updated on 09/Oct/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Commented by I want to learn more last updated on 09/Oct/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by 1549442205PVT last updated on 09/Oct/20
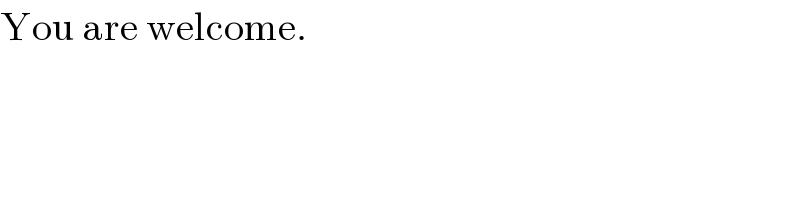
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
