
Question Number 182922 by mnjuly1970 last updated on 16/Dec/22
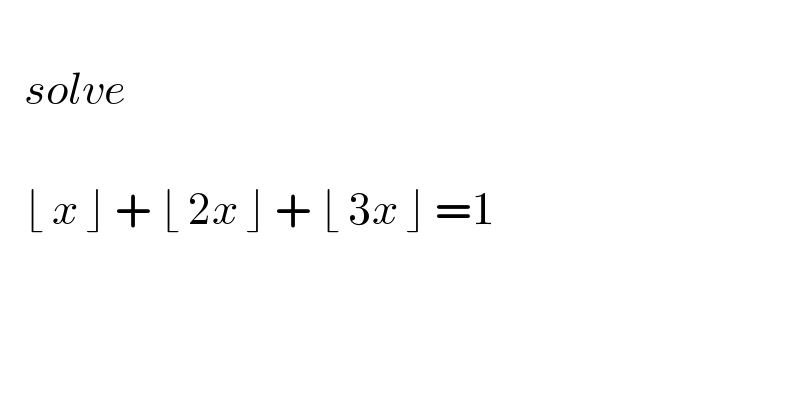
$$ \\ $$$$\:\:\:{solve} \\ $$$$ \\ $$$$\:\:\:\lfloor\:{x}\:\rfloor\:+\:\lfloor\:\mathrm{2}{x}\:\rfloor\:+\:\lfloor\:\mathrm{3}{x}\:\rfloor\:=\mathrm{1} \\ $$$$ \\ $$
Answered by mr W last updated on 16/Dec/22
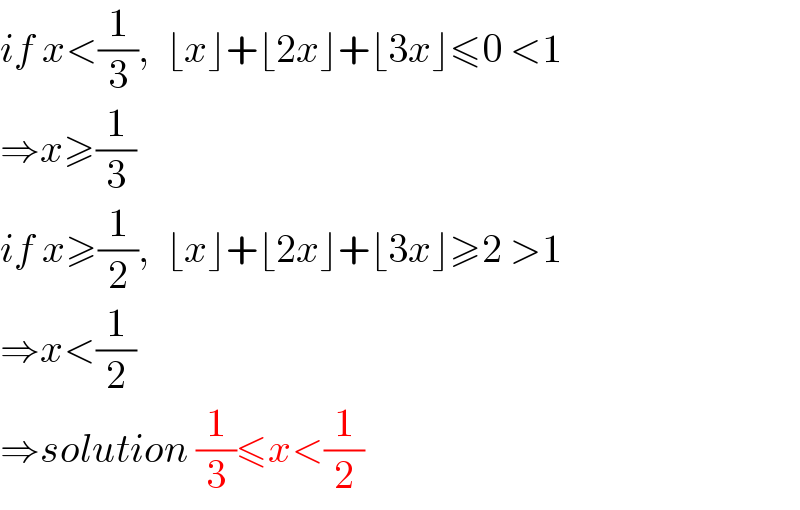
$${if}\:{x}<\frac{\mathrm{1}}{\mathrm{3}},\:\:\lfloor{x}\rfloor+\lfloor\mathrm{2}{x}\rfloor+\lfloor\mathrm{3}{x}\rfloor\leqslant\mathrm{0}\:<\mathrm{1} \\ $$$$\Rightarrow{x}\geqslant\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${if}\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}},\:\:\lfloor{x}\rfloor+\lfloor\mathrm{2}{x}\rfloor+\lfloor\mathrm{3}{x}\rfloor\geqslant\mathrm{2}\:>\mathrm{1} \\ $$$$\Rightarrow{x}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{solution}\:\frac{\mathrm{1}}{\mathrm{3}}\leqslant{x}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 17/Dec/22
$$\:{very}\:{nice}\:{and}\:{short}\: \\ $$
