
Previous in Differential Equation Next in Differential Equation
Question Number 126285 by bramlexs22 last updated on 19/Dec/20
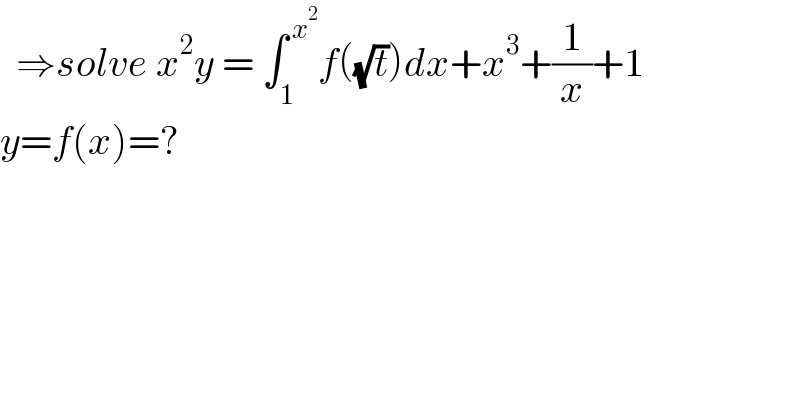
$$\:\:\Rightarrow{solve}\:{x}^{\mathrm{2}} {y}\:=\:\int_{\mathrm{1}} ^{\:{x}^{\mathrm{2}} } {f}\left(\sqrt{{t}}\right){dx}+{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}}+\mathrm{1} \\ $$$${y}={f}\left({x}\right)=? \\ $$
Answered by liberty last updated on 19/Dec/20
![⇒ (d/dx) [ x^2 y ] = (d/dx) [ ∫_1 ^( x^2 ) f((√t))dt +x^3 +x^(−1) +1 ] ⇒2xy+x^2 (dy/dx) = 2xf(x)+3x^2 −x^(−2) ⇒2xy+ x^2 (dy/dx) = 2xy + 3x^2 −x^(−2) ⇒ x^2 (dy/dx) = 3x^2 −x^(−2) ⇒ (dy/dx) = 3−x^(−4) ⇒ y=∫(3−x^(−4) )dx ⇒ y=3x+(1/(3x^3 ))+C](Q126286.png)
$$\Rightarrow\:\frac{{d}}{{dx}}\:\left[\:{x}^{\mathrm{2}} {y}\:\right]\:=\:\frac{{d}}{{dx}}\:\left[\:\int_{\mathrm{1}} ^{\:{x}^{\mathrm{2}} } {f}\left(\sqrt{{t}}\right){dt}\:+{x}^{\mathrm{3}} +{x}^{−\mathrm{1}} +\mathrm{1}\:\right] \\ $$$$\Rightarrow\mathrm{2}{xy}+{x}^{\mathrm{2}} \:\frac{{dy}}{{dx}}\:=\:\mathrm{2}{xf}\left({x}\right)+\mathrm{3}{x}^{\mathrm{2}} −{x}^{−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{xy}+\:{x}^{\mathrm{2}} \:\frac{{dy}}{{dx}}\:=\:\mathrm{2}{xy}\:+\:\mathrm{3}{x}^{\mathrm{2}} −{x}^{−\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \:\frac{{dy}}{{dx}}\:=\:\mathrm{3}{x}^{\mathrm{2}} −{x}^{−\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}\:=\:\mathrm{3}−{x}^{−\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\int\left(\mathrm{3}−{x}^{−\mathrm{4}} \right){dx} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{3}} }+{C}\: \\ $$
