
Question Number 172030 by Mikenice last updated on 23/Jun/22
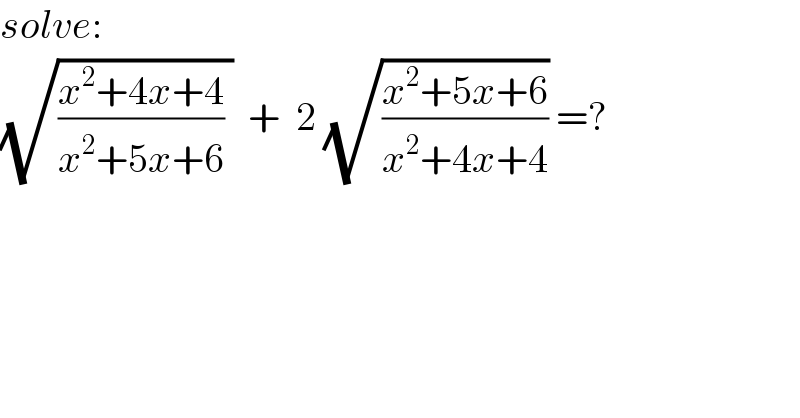
$${solve}: \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}}\:}\:\:+\:\:\mathrm{2}\:\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}\:=? \\ $$
Answered by Rasheed.Sindhi last updated on 23/Jun/22
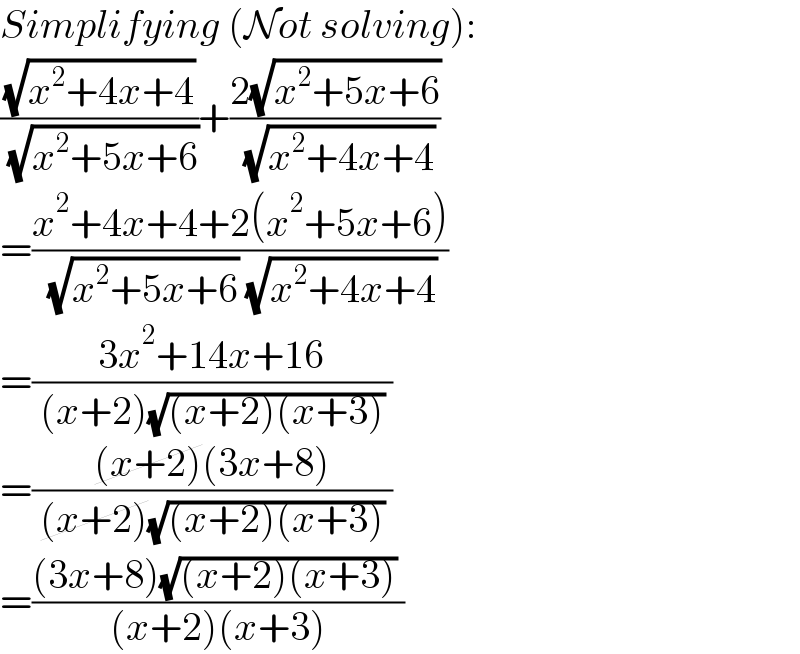
$${Simplifying}\:\left(\mathcal{N}{ot}\:{solving}\right): \\ $$$$\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}}}+\frac{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}} \\ $$$$=\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}} \\ $$$$=\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{16}}{\:\left({x}+\mathrm{2}\right)\sqrt{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:} \\ $$$$=\frac{\cancel{\left({x}+\mathrm{2}\right)}\left(\mathrm{3}{x}+\mathrm{8}\right)}{\:\cancel{\left({x}+\mathrm{2}\right)}\sqrt{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:} \\ $$$$=\frac{\left(\mathrm{3}{x}+\mathrm{8}\right)\sqrt{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:}{\:\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)\:} \\ $$
Commented by Mikenice last updated on 23/Jun/22

$${thanks}\:{sir} \\ $$
