
Question Number 188034 by Michaelfaraday last updated on 25/Feb/23
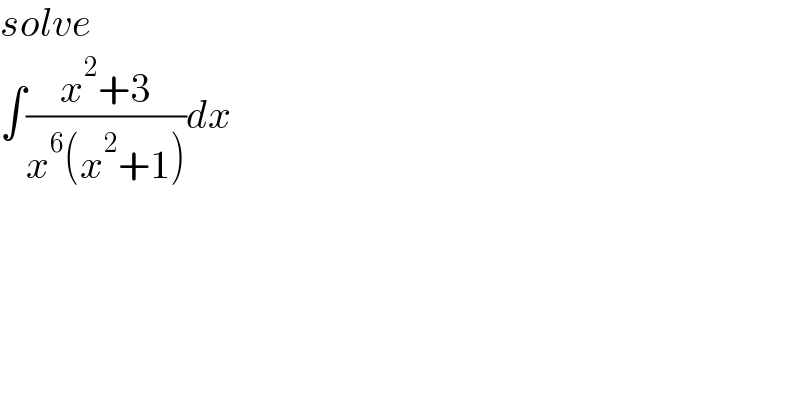
$${solve} \\ $$$$\int\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}^{\mathrm{6}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$
Answered by MJS_new last updated on 25/Feb/23
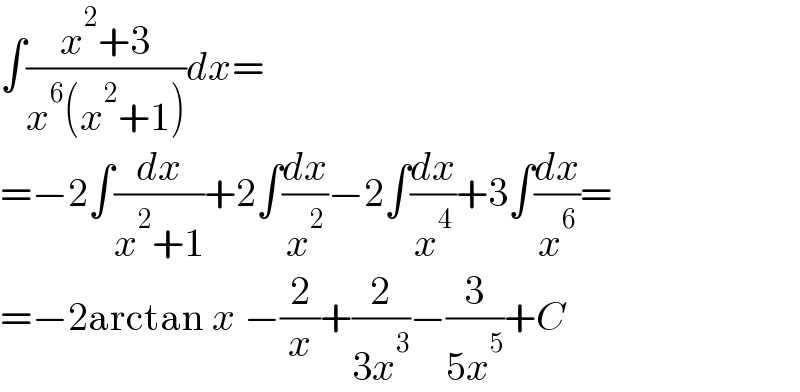
$$\int\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}^{\mathrm{6}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$=−\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{2}} }−\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{4}} }+\mathrm{3}\int\frac{{dx}}{{x}^{\mathrm{6}} }= \\ $$$$=−\mathrm{2arctan}\:{x}\:−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{5}{x}^{\mathrm{5}} }+{C} \\ $$
Commented by Michaelfaraday last updated on 01/Mar/23

$${thanks}\:{sir} \\ $$
