
Question Number 99319 by M±th+et+s last updated on 20/Jun/20
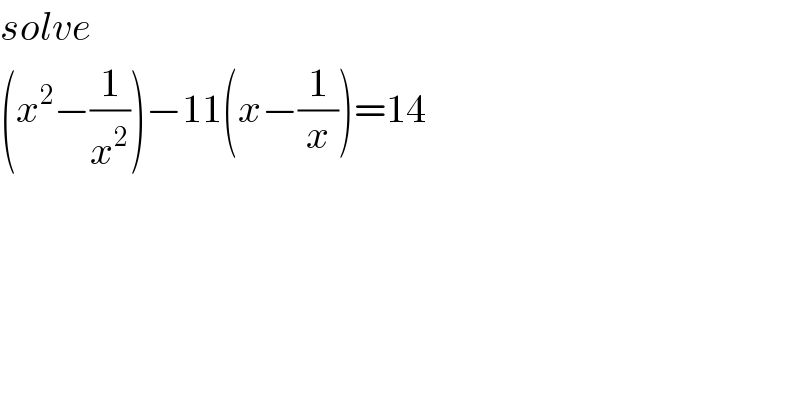
$${solve} \\ $$$$\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{11}\left({x}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{14} \\ $$
Answered by behi83417@gmail.com last updated on 20/Jun/20
![x−(1/x)=t⇒(x+(1/x))^2 =(x−(1/x))^2 +2=t^2 +2 t(√(t^2 +2))−11t=14⇒t(√(t^2 +2))=11t+14 ⇒t^2 (t^2 +2)=121t^2 +308t+196 ⇒t^4 −119t^2 −308t−196=0 ⇒t=[−9.41,−1.57,−1.1,12.077] { ((x−(1/x)=−9.41⇒x^2 +9.41x−1=0)),((⇒x=((−9.41±(√(9.41^2 +4)))/2)=0.11,−9.5)) :} { ((x−(1/x)=−1.57⇒x^2 +1.57x−1=0)),((⇒x=((−1.57±(√(1.57^2 +4)))/2)=0.49,−2.1)) :} { ((x−(1/x)=−1.1⇒x^2 +1.1x−1=0)),((⇒x=((−1.1±(√(1.1^2 +4)))/2)=0.6,−1.7)) :} { ((x−(1/x)=12.1⇒x^2 −12.1x−1=0)),((⇒x=((12.1±(√(12.1^2 +4)))/2)=12.18,−0.082)) :}](Q99373.png)
$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\Rightarrow\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} =\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}=\mathrm{t}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{2}}−\mathrm{11t}=\mathrm{14}\Rightarrow\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{2}}=\mathrm{11t}+\mathrm{14} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{121t}^{\mathrm{2}} +\mathrm{308t}+\mathrm{196} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{4}} −\mathrm{119t}^{\mathrm{2}} −\mathrm{308t}−\mathrm{196}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}=\left[−\mathrm{9}.\mathrm{41},−\mathrm{1}.\mathrm{57},−\mathrm{1}.\mathrm{1},\mathrm{12}.\mathrm{077}\right] \\ $$$$\begin{cases}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{9}.\mathrm{41}\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{9}.\mathrm{41x}−\mathrm{1}=\mathrm{0}}\\{\Rightarrow\mathrm{x}=\frac{−\mathrm{9}.\mathrm{41}\pm\sqrt{\mathrm{9}.\mathrm{41}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}=\mathrm{0}.\mathrm{11},−\mathrm{9}.\mathrm{5}}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{1}.\mathrm{57}\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{1}.\mathrm{57x}−\mathrm{1}=\mathrm{0}}\\{\Rightarrow\mathrm{x}=\frac{−\mathrm{1}.\mathrm{57}\pm\sqrt{\mathrm{1}.\mathrm{57}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}=\mathrm{0}.\mathrm{49},−\mathrm{2}.\mathrm{1}}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{1}.\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{1}.\mathrm{1x}−\mathrm{1}=\mathrm{0}}\\{\Rightarrow\mathrm{x}=\frac{−\mathrm{1}.\mathrm{1}\pm\sqrt{\mathrm{1}.\mathrm{1}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}=\mathrm{0}.\mathrm{6},−\mathrm{1}.\mathrm{7}}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{12}.\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{12}.\mathrm{1x}−\mathrm{1}=\mathrm{0}}\\{\Rightarrow\mathrm{x}=\frac{\mathrm{12}.\mathrm{1}\pm\sqrt{\mathrm{12}.\mathrm{1}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}=\mathrm{12}.\mathrm{18},−\mathrm{0}.\mathrm{082}}\end{cases} \\ $$
