
Question Number 64153 by meme last updated on 14/Jul/19
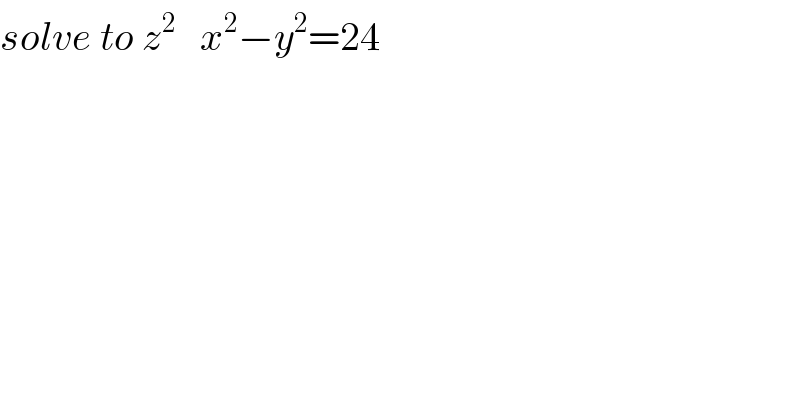
$${solve}\:{to}\:{z}^{\mathrm{2}} \:\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{24} \\ $$
Answered by mr W last updated on 15/Jul/19
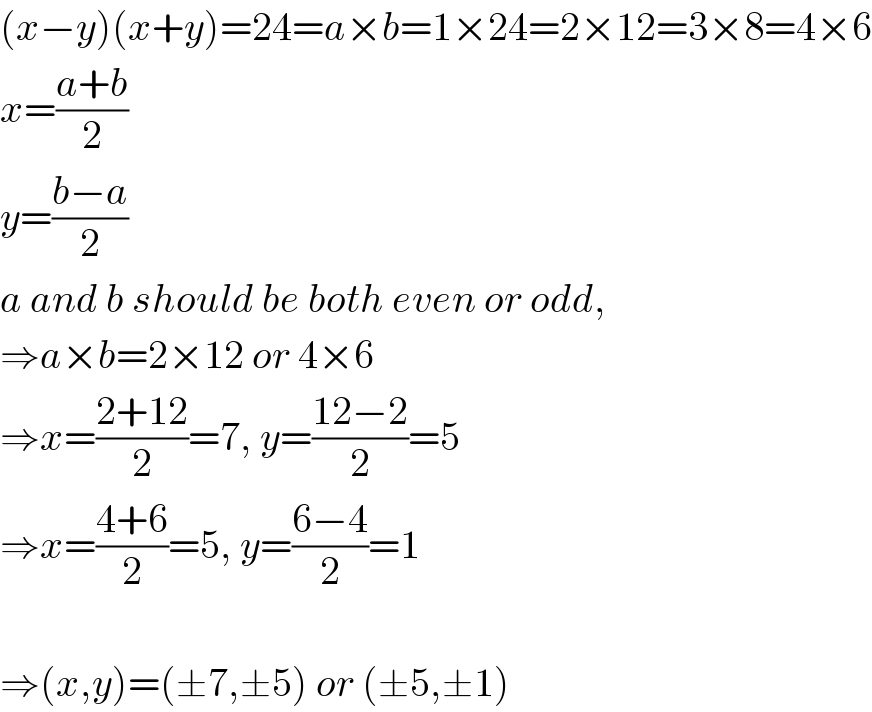
$$\left({x}−{y}\right)\left({x}+{y}\right)=\mathrm{24}={a}×{b}=\mathrm{1}×\mathrm{24}=\mathrm{2}×\mathrm{12}=\mathrm{3}×\mathrm{8}=\mathrm{4}×\mathrm{6} \\ $$$${x}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$${y}=\frac{{b}−{a}}{\mathrm{2}} \\ $$$${a}\:{and}\:{b}\:{should}\:{be}\:{both}\:{even}\:{or}\:{odd}, \\ $$$$\Rightarrow{a}×{b}=\mathrm{2}×\mathrm{12}\:{or}\:\mathrm{4}×\mathrm{6} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}+\mathrm{12}}{\mathrm{2}}=\mathrm{7},\:{y}=\frac{\mathrm{12}−\mathrm{2}}{\mathrm{2}}=\mathrm{5} \\ $$$$\Rightarrow{x}=\frac{\mathrm{4}+\mathrm{6}}{\mathrm{2}}=\mathrm{5},\:{y}=\frac{\mathrm{6}−\mathrm{4}}{\mathrm{2}}=\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\pm\mathrm{7},\pm\mathrm{5}\right)\:{or}\:\left(\pm\mathrm{5},\pm\mathrm{1}\right) \\ $$
