
Question Number 63383 by minh2001 last updated on 03/Jul/19
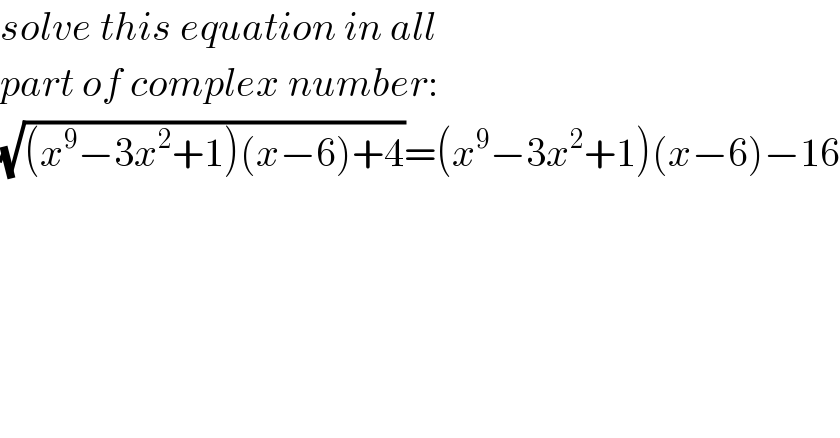
$${solve}\:{this}\:{equation}\:{in}\:{all}\: \\ $$$${part}\:{of}\:{complex}\:{number}: \\ $$$$\sqrt{\left({x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)+\mathrm{4}}=\left({x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)−\mathrm{16} \\ $$
Commented by MJS last updated on 04/Jul/19

$$\mathrm{waiting}\:\mathrm{to}\:\mathrm{see}\:\mathrm{your}\:\mathrm{solution} \\ $$
Answered by MJS last updated on 03/Jul/19

$$\sqrt{{t}+\mathrm{4}}={t}−\mathrm{16} \\ $$$${t}+\mathrm{4}=\left({t}−\mathrm{16}\right)^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} −\mathrm{33}{t}+\mathrm{252}=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\mathrm{12}\vee{t}=\mathrm{21} \\ $$$$\mathrm{but}\:{t}=\mathrm{12}\:\mathrm{is}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{of}\:\sqrt{{t}+\mathrm{4}}={t}−\mathrm{16} \\ $$$$\Rightarrow\:{t}=\mathrm{21} \\ $$$$\left({x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)=\mathrm{21} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{9}} −\mathrm{7}{x}^{\mathrm{8}} +\mathrm{7}{x}^{\mathrm{7}} −\mathrm{7}{x}^{\mathrm{6}} +\mathrm{7}{x}^{\mathrm{5}} −\mathrm{7}{x}^{\mathrm{4}} +\mathrm{7}{x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{28}{x}−\mathrm{27}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{cannot}\:\mathrm{exactly}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{rest} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{6}.\mathrm{00000208} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{8}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{complex}\:\left(\mathrm{4}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{conjugated}\:\mathrm{complex}\:\mathrm{roots}\right) \\ $$$$\mathrm{if}\:\mathrm{it}'\mathrm{s} \\ $$$$\sqrt{\left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)+\mathrm{4}}=\left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)−\mathrm{16} \\ $$$$\mathrm{we}\:\mathrm{can}: \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{6}\right)=\mathrm{21} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{28}{x}−\mathrm{27}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{10}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}−\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}+\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{10}}{\mathrm{3}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}−\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}+\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}} \\ $$$${x}_{\mathrm{4}} =\frac{\mathrm{10}}{\mathrm{3}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}−\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\frac{\mathrm{209}}{\mathrm{54}}+\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}} \\ $$
Commented by minh2001 last updated on 04/Jul/19
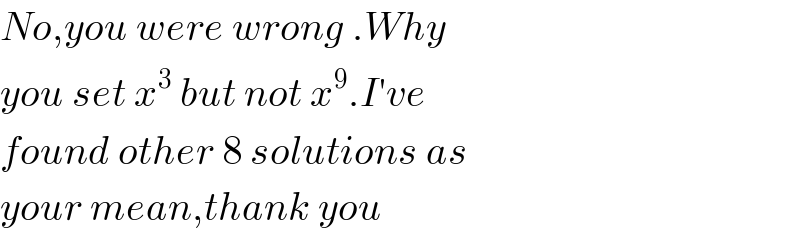
$${No},{you}\:{were}\:{wrong}\:.{Why} \\ $$$${you}\:{set}\:{x}^{\mathrm{3}} \:{but}\:{not}\:{x}^{\mathrm{9}} .{I}'{ve} \\ $$$${found}\:{other}\:\mathrm{8}\:{solutions}\:{as} \\ $$$${your}\:{mean},{thank}\:{you} \\ $$
Commented by MJS last updated on 04/Jul/19

$$\mathrm{so}\:\mathrm{show}\:\mathrm{us}\:\mathrm{how}\:\mathrm{you}\:\mathrm{found}\:\mathrm{them} \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{approximate}\:\mathrm{them}\:\mathrm{all} \\ $$
Commented by MJS last updated on 04/Jul/19

$$\mathrm{with}\:{x}^{\mathrm{9}} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{6}.\mathrm{00000208383} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \approx−.\mathrm{994927692081}\pm.\mathrm{650751638656i} \\ $$$${x}_{\mathrm{5},\:\mathrm{6}} \approx−.\mathrm{262576070729}\pm\mathrm{1}.\mathrm{25073913893i} \\ $$$${x}_{\mathrm{7},\:\mathrm{8}} \approx.\mathrm{684103814572}\pm\mathrm{1}.\mathrm{04916880346i} \\ $$$${x}_{\mathrm{9},\:\mathrm{10}} \approx\mathrm{1}.\mathrm{07339890633}\pm.\mathrm{300735402858i} \\ $$
